区块链技术及应用期末复习
区块链技术及应用期末复习
15单选+10填空+5问答题+2计算
参考区块链技术指南
第1章 区块链的诞生
1.1 区块链诞生的背景
- 记账技术:是金融技术这一支柱最核心的基石,人类发展伴随着记账科技的持续演化
- 资产:可以被拥有和控制来产生价值的东西
- 账本:
- 账本:存储记录的系统
- 交易:资产通过账本转入或转出
- 合约:交易发生的条件
- 记账技术的演化
- 单式账本:通过单条记录进行账目记录的方法;容易出错、难定位问题、只保管记账者手里
- 复式账本:将单一中心记录拆成多个科目,包括增减记账法、收付记账法、借贷记账法。
- 数字化账本:随着计算机和数据库的出现,使账本规模、处理速度、账本复杂度巨大改变。
- 以上三个都是中心化模式的账本,存在的问题:低效(使用多种不同的协议)、昂贵(协调费用)、脆弱
- 分布式账本:交易多方共同维护一个共享的分布式账本
- “中本聪”发表了一篇 文章 “比特币:一种点对点电子现金系统 ”,系统的核心就是分布式账本技术,称为“区块链”。
- 分布式记账的难题:一旦有某参与方恶意篡改已发生的记录,则无法保证记录的正确性。
- 改进:带有数字摘要的分布式记账结构
1.2 区块链的基本概念
区块链的类型
公链:任何人都可以参与或者离开
联盟链:节点需被认证,且节点属于不同组织
私有链:节点需被认证,且节点属于同一组织
许可链:联盟链和私有链属于许可链,指参与到区块链系统中的每个节点都是经过许可
非许可链:公链属于非许可链
主链:由公共账本构成的数据链
侧链:依托并连接主链的数据链
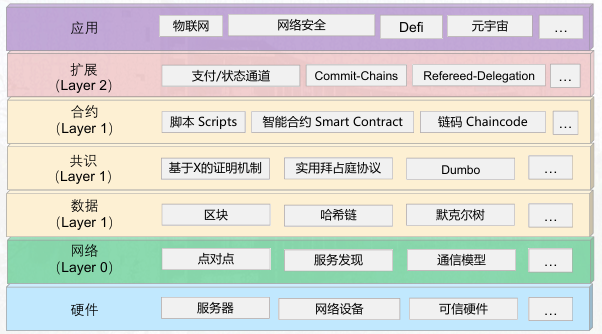
区块链的层级结构
三次浪潮
- 区块链1.0:2013,比特币(Bitcoin)为代表的加密货币。
- 区块链2.0:2016,以以太坊(Ethereum)为代表金融应用。
- 区块链3.0:2017,区块链技术用于多种应用场景和行业
1.3 区块链的价值基础
- 区块链和生产力与生产关系
- 生产力:社会成员共同改造自然、改造社会获取生产资料和生活资料的能力。
- 生产关系:个体或组织的价值创造、价值交互与价值记录的过程。
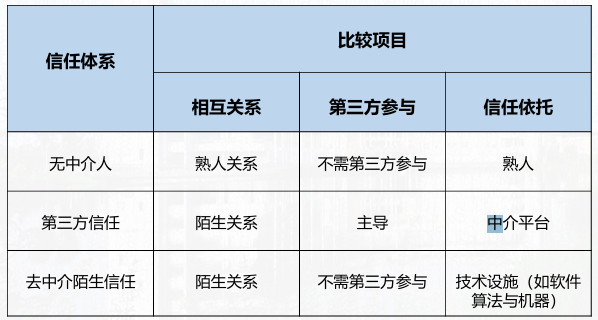
- 信任体系
- 区块链价值基础包含三大根本关系
- 所有关系:人类社会生产关系的根本关系
- 交易关系:人类社会活动的本质
- 历史关系:在人类价值创造、交易变更等活动中,形成了按时间顺序且不可逆的活动过程记录
- 区块链构建了价值传递网络
- 区块链服务网络:区块链开放的分层技术架构体系使得开发者可根据服务定位不同、服务目标不同、应用场景不同等,创新形成各种类型的服务运营网络
- 区块链价值生态系统:基于区块链服务网络,可以围绕不同的产业或应用主题,构建变革性的价值生态系统。
1.4 区块链的应用与挑战
- 区块链的应用
- 解决的核心问题:去中介陌生信任体系的构建
- 技术本质:基于社群共识创建和维护一个全局统一的公共账本。
第2章 区块链核心技术概览
2.1 分布式记账的难点
如何保证交易的合法性?防止女巫攻击
比特币的交易流程
- 交易启动:发送者决定将比特币发送给接收者。他们需要收件人的公共地址(类似于比特币的电子邮件地址)以及他们希望发送的金额。
- 交易创建:发送者使用钱包输入接收者的地址和要发送的比特币金额。然后钱包创建一个交易,该交易本质上是一条消息,表明发送者希望将比特币转移到接收者的地址。
- 签署交易:交易使用发送者的私钥进行签名。该数字签名证明发送者拥有他们希望发送的比特币,而无需泄露私钥。这类似于在传统银行系统中签署支票,但经过安全加密。
- 广播交易:一旦签名,交易就会被广播到比特币网络,由节点接收并在整个网络中传播。这就像向网络宣布发送者希望将比特币转移给接收者。
- 验证和验证:网络上的矿工从内存池中收集交易,并开始通过挖掘来验证它们的过程。这涉及检查数字签名以确保交易是真实的并且发送者有足够的余额来完成交易。
- 挖掘交易:矿工们竞相解决密码难题,这涉及大量的计算工作。第一个解决这个难题的矿工可以将一个交易块(包括发送者发起的交易)添加到区块链中。添加区块的行为可以确认交易并使其不可逆转。
- 交易确认:一旦交易被包含在区块中并添加到区块链中,就被视为已确认。接收者的钱包注意到交易已被确认,并更新余额以反映收到的比特币。
2.2 比特币的五大核心问题
- 每个全节点维护着一份账本的拷贝, 为什么节点愿意帮忙?
- 激励,奖励。挖矿费,交易费
- 挖矿费:从50个比特币开始,每四年减半。总共约为21,000,000,两千一百万
- 每个全节点都可以提出一个区块, 那么到底选择谁的呢?
- 工作量证明机制(PoW):让每个节点解一个难题
- 问题很难、唯一方法是暴力破解、投入资源是CPU算力
- 哈希算法:单向性、弱抗碰撞性、强抗碰撞性
- 弱抗碰撞性和强抗碰撞性的区别在于:弱抗碰撞性是任意给定分组x, 寻求不等于x的x’, 使得H(x)= H(x’)在计算上不可行;强抗碰撞性是寻求任何的(x,x’)对,使得H(x)=H(x’)在计算上不可行; 前者的x是给定的,而后者是不给定的,因而强抗碰撞性的要求要比弱抗碰撞性的要求的要高。
- 工作量证明机制(PoW):让每个节点解一个难题
- 如何实现交易防伪,即保证比特币的交易是真实的?
- 数字签名
- 如何解决“余额检查”及“双重支付”?
- 余额检查
- 如何防⽌交易被恶意篡改?
- 最长链原则
2.3 区块链的架构与功能
区块(Block):大小:不超过1MB,交易数:~4000条
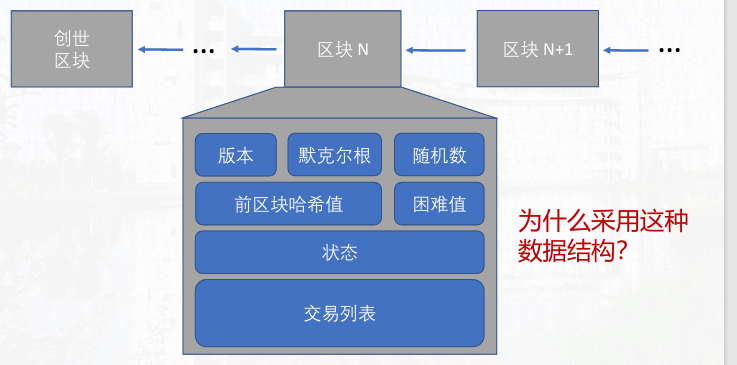
- 链式结构:每个区块的区块头中都包含了前一区块的哈希值(摘要),从而形成一条不可更改的完整区块数据链。
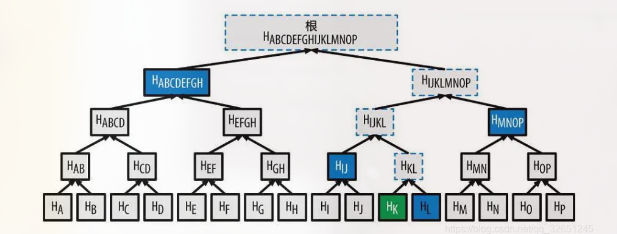
- 默克尔树(Merkle)
- 每条交易的哈希值就是一个叶子节点,形成二叉树
- 快速比较大量数据:当两个默克尔树根相同时,则意味着所代表的数据必然相同
- 快速定位修改:如果 D1 中数据被修改,可以通过路径快速定位
- 零知识证明:证明一组交易中包含某个交易A,但不让对方知道交易A的具体内容
- 共识算法
- 停⽌性(Termination) 共识协议能够在多项式时间内停⽌
- ⼀致性(Agreement) 共识协议能够保证所有诚实节点的状态⼀致
- 安全性(Safety) ⼀致的状态来⾃于某个诚实的节点的提议。
2.4 典型的区块链平台
- 比特币(Bitcoin)、以太坊(Ethereum)、超级账本(Hyperledger Fabric)、FISCO BCOS
2.5 区块链典型应用场景概览
- 数字货币(Cryptocurrency)
- 供应链(Supply Chain)
- 资源共享(Resource Sharing)
- 众筹(CrowdFunding)
- 等等
第3章 分布式系统核心技术
3.1 一致性问题
定义:在分布式系统领域指对于多个服务节点,给定一系列操作,在约定协议的保证下,使得它们对处理结果达成“某种程度”的协同。
一致性的要求
- 可中止性(termination):一致的结果在有限时间内完成。
- 约同性(agreement):不同节点最终完成决策的结果是相同的
- 合法性(safety):决策的结果必须是某个节点提出的提案。
强一致性:顺序一致性(线程见到的顺序指定)、线性一致性(线性一致性还保证节点间的事件先后顺序);弱一致性
一致性 VS. 共识
- 一致性指多个副本对外呈现的状态,如顺序一致性、线性一致性,描述了多节点对数据状态的共同维护能力
- 共识特指在分布式系统中多个节点对某个事情(如多个事务请求,先执行谁?)达成一致看法的过程
3.2 共识算法
- 故障容错(CFT) :Paxos算法(1990年) 、Raft算法(2014年)
- 拜占庭容错(BFT): PBFT算法(1999年)、 PoW算法(1997年)
3.3 FLP不可能原理
FLP不可能原理:在网络可靠但允许节点失效(即便只有一个)的最小化异步模型系统中,不存在一个可以解决一致性问题的确定性共识算法
不要浪费时间,去为异步分布式系统设计在任意场景下都能实现共识的算法。
3.4 CAP原理
- C(Consistency)一致性:任何事务都是原子的,所有副本的状态都是事务成功提交后的结果,并保持强一致。
- A(Availability)可用性:系统(非失败节点)能在有限时间内完成对操作请求 的应答。
- P(Partition)分区容忍性:系统中的网络可能发生分区故障(成为多个子网, 甚至出现节点上线和下线),即节点间的通信无法保障;而网络故障不应该影响 到系统正常服务
CAP原理认为:分布式系统最多只能保证以上三个特性中的两个
- 应用场景
- 弱化一致性:对结果一致性不敏感的应用,可以允许在新版本上线后过一段时 间才能最终更新成功,期间不保证一致性。例如:网站静态页面、实时性较弱的查询
- 弱化可用性:对结果一致性很敏感的应用,比如银行取款机,当系统出现故障 时会拒绝服务。例:银行取款机
- 弱化分区容忍性:出现网络分区的概率很小,两阶段的提交算法、双通道等机制增强可靠性解决
3.5 ACID原则
ACID原则描述了分布式数据库需要满足的一致性需求,同时允许付出可用性的代价。
- A(Atomicity)原子性:每次事务都是原子的,事务包含的所有操作要么全部执行成功,要么全部不执行。一旦操作失败,需要回退状态到执行事务之前。
- C(Consistency)一致性:数据库的状态在事务执行前后是一致的和完整的,无中间状态,即只能处于成功事务提交后的状态。
- I(Isolation)隔离性:各种事务可以并发执行,但彼此之间互相不影响。
- D(Durability)持久性:状态的改变是持久的,不会失效。一旦某个事务提交,它造成的状态变更就是永久性的。
第4章 区块链共识协议
4.2 Paxos和Raft共识协议
- Paxos共识算法:从工程的角度实现了一种最大化保障分布式系统一致性的机制
- Raft共识协议 :(1)领导者选举;(2)同步日志。领导者定期发送心跳信息。
4.3 拜占庭将军问题
- 多少个叛徒可以被容忍?
- 对于3f+1个将军,如果有大于f个叛徒,此问题无解
4.4 PBFT共识协议
- 如果将军数为 n、叛将数为 f,那么算法需要递归协商 f+1 轮,消息复杂度为 O(n ^ (f + 1))
第5章 密码学技术
5.2 对称加解密及消息认证码
对称加解密:加密和解密用到的密钥是相同的,算法公开,密钥保密
对称加解密语法,接口,参数
- Gen:概率性算法,产生一把秘钥 k \(k \gets Gen(1^n)\)
- Enc:利用秘钥k,对信息m进行加密,输出密文c \(c \gets Enc_k(m)\)
- Dec:利用秘钥k,对密文c进行解密,输出原文m \(m :=Eec_k(c)\)
- 安全特性:正确性(Correctness) \(\mathrm{Dec}_k(Enc_k(m))=m\)
柯克霍夫(Kerckhoffs)原则:密码系统应该就算被所有人知道系统的运作步骤,仍然是安全的。
现代密码学的三大原则
- 正式的定义(Formal Definition)
- 准确的假设(Precise Assumption)
- 安全性的证明(Proof of Security)
安全等级:攻击强度递增,难度递减
- 唯密文攻击 Cipher-only attack :只知道密文,推出明文或密钥,一般用穷举攻击。
- 已知明文攻击 Known-plaintext attack :知道部分的明文和密文对,推出密钥和加密算法。
- 选择明文攻击 Chosen-plaintext attack :知道明文就知道密文,目标为推出密钥
- 选择密文攻击 Chosen-ciphertext attack :知道密文就知道明文,目标为推出密钥。
One-Time Pad (OTP)加密算法
- 完美安全的加密方案,在认证过程中仅使用一次的密码。一旦使用,该密码立即失效,不能重复使用。
- 算法:
- 固定一个整数l>0,消息,密钥和密文长度为\(l\) |M| = |K| = |C|,
- Gen密钥生成算法:会根据均匀分布,从密钥空间中选择一个密钥。
- Enc加密算法:明文和密钥满足 \(m,k \in \{0,1\}^l\) 加密为 \(c = m \oplus k\)
- Dec解密算法: \(m = c \oplus k\)
对称加密(SE)常见算法:DES、3DES、AES
消息认证码
- 消息认证码的语法
- k = Gen(𝜆) 密钥生成算法,安全参数𝜆(例如,密钥的长度),生成随机的、足够强度的密钥
- t = Mac(k, m) 标签生成算法,利用密钥k对消息m进行加密运算,生成一个唯一的标签t(也称为MAC值)
- b = Vrfy(m, t) 标签验证算法,使用已知的消息m和收到的标签t,通过重新计算MAC值并与t进行比较,b为0或1(验证成功)
- 消息认证码的语法
5.3 RSA与椭圆曲线算法
- 非对称加密
- 非对称加解密
- 数字签名
- 欧拉函数在\(\{0,1,\cdots,m-1\}\)
中,与m互质的整数的个数表示为𝜑(𝑚)。
- m非常大的时候的计算法:
- 考虑 m 有如下的分解: \[\mathfrak{m}=p_1^{e_1}\cdot p_2^{e_2}\cdot\cdots\cdot p_n^{e_n}\] 其中 p\(_i\)是不同的质数,\(\mathrm e_i\)是整数,那么: \[\begin{aligned}&\varphi(\mathfrak{m})=\prod_{i=1}^n(p_i^{e_i}-p_i^{e_i-1})\end{aligned}\]
- 当m是素数时,φ=m-1
- 当n可以分解成两个互质的整数之积,n = p1 × p2,则φ(n) = φ(p1p2) = φ(p1)φ(p2)
- m非常大的时候的计算法:
- RSA
- 密钥生成Gen过程:
- 选择两个大素数 p, q
- 计算 \(n=p\cdot q\)
- 计算 \(\varphi(n)=(p-1)\cdot(q-1)\)
- 选择公钥 pk 为:e\(\in\{1,2,...,\varphi(n)-1\}\),使得 gcd\((e,\varphi(n))=1\) 互质
- 计算私钥 sk为:d,使得 d\(\cdot\)e\(\equiv1\mod \varphi(n)\) 乘法逆元
- 密钥对(pk,sk) 为:((n,e),d)
- 加密过程Enc
- 给定公钥 (𝑛,𝑒),以及待加密信息 𝑥∈𝑍 ={0,1,…,𝑛−1}
- 计算密文为: \(y=x^e\mod n\)
- 解密过程Dec
- 给定私钥 d,以及密文 y∈𝑍 ={0,1,…,𝑛−1}
- 计算解密后的明文为:\(x=y^d\mod n\)
- 密钥生成Gen过程:
- 椭圆曲线加密了解
5.4 Diffie-Hellman密钥交换
- 是一种加密协议,允许两个从未见过面的参与方在不安全的通信信道上共同生成一个共享的秘密密钥。这个密钥随后可以用于对称加密
- 参数选择:
- 公共参数:素数 $ p $ 和生成元 $ g $,这两个值是公开的。
- 密钥交换步骤:
- Alice和Bob分别选择私钥:
- Alice选择一个私有密钥 $ a $(一个大随机整数)。
- Bob选择一个私有密钥 $b $(一个大随机整数)。
- 计算公钥:
- Alice计算她的公钥 $ A = g^a p $ 并将其发送给Bob。
- Bob计算他的公钥 $B = g^b p $ 并将其发送给Alice。
- 计算共享密钥:
- Alice接收到Bob的公钥后,计算共享密钥 $ s = B^a p $。
- Bob接收到Alice的公钥后,计算共享密钥 $ s = A^b p$。
- 根据模幂运算的性质,Alice和Bob计算出的共享密钥 $ s $ 是相同的,即 $ s = g^{ab} p $。
- Alice和Bob分别选择私钥:
5.5 t-out-of-n秘密共享协议
- 概念:秘密共享的核心思想是将秘密拆分为n份,分别分发给参与方,n-out-of-n秘密共享要求所有参与方结合才能恢复秘密,t-out-of-n秘密共享要求至少任意t个参与方结合才能恢复秘密。
- 由分发算法 Share(s, t, n) -> {\(s_1,s_2,\dots,s_n\)} 和秘密重构算法 Reconstruct(\(s_1,s_2,\dots,s_t\)) -> s 组成
- 基于线性代数的秘密共享
- 分发算法 Share(s, t, n)
- 选择t-1个随机数以及秘密s一起构造多项式\(f(x) = s+a_1x+a_2x^2+\cdots+a_{t-1}x^n\),\(a_0=s\)!
- 任取n个数\(x_1,x_2,\dots,x_n\)对于n个参与方,每个人的密钥是\((x_i,f(x_i))\)
- 重构算法 Reconstruct(\(s_1,s_2,\dots,s_t\))
- 知道t个密钥就可以重新计算\([s,a_1,a_2,\dots]\)
- 分发算法 Share(s, t, n)
5.6 数字证书、PKI体系与TLS协议
了解
5.7 高阶密码学知识(ZKP、SMPC、VRF、OT、HE、FL)
- 零知识证明:证明者(Prover)能够在不向验证者(Verifier)提供任何有用信息的情况下,使验证者相信某个论断是正确的。
- 安全多方计算:多个参与方在不泄露各自私有数据的前提下,共同计算一个函数的结果。
- 可验证随机函数:结合了伪随机函数和数字签名的特性
- 不经意传输:允许发送方(Sender)向接收方(Receiver)传输一个消息集合中的一个消息,而接收方只能获取其中一个消息,并且发送方不知道接收方获取的是哪一个
- 同态加密:对密文数据的操作等价于对明文操作的结果进行加密
- 联邦学习:分布式机器学习方法,允许多个参与方在不共享各自数据的前提下,共同训练一个机器学习模型
- 横向联邦学习:特征相似、样本不同
- 纵向联邦学习:样本相同、特征不同
- 联邦迁移学习:都不同
零知识证明 地图三染色问题 过程 利用零知识证明证明 过程会
机密交易 了解
第6章 区块链平台框架
6.1 典型区块链平台框架
6.2 比特币 Bitcoin
6.3 以太坊 Ethereum
6.4 超级账本 Hyperledger Fabric
6.5 FISCO BCOS
特点、结局了哪些问题、有哪些结点、交易流程