计算机图形学 - 期末复习
计算机图形学理论课复习大纲
考试题型:简答题,计算题,绘图题,分析与设计题,程序实现题。
分数分别为:20分,30分,10分,30分,10分。
一、 图形学基本概念
- 什么是计算机图形学?
- 计算机图形学的主要研究内容包括哪些?
- 计算机图形学的主要应用领域。
- 图形和图像的主要区别是什么?
- 计算机图形处理系统的主要构成。
- 显卡的工作流程。
- 什么是显示存储器?
- GPU的基本概念。
- 显卡分辨率的含义。
- GPU堆包含哪几种主要的类型,具有什么样的特点?
- GPU渲染流水线包含哪几个阶段,分别完成什么任务?
- 光照的基本原理
- 光照模型的分类
- 光源的分类
- 纹理的表现形式。
- 纹理的过滤方式及寻址方式
- 多级纹理的基本原理
- 模型的表示方法
- Direct3D 12图形绘制的基本原理
- 三维模型顶点的数据结构表示
二、 图形学基本算法
要求:算法的基本原理,算法描述,算法执行过程分析,过程计算,编程实现等。
- 直线生成算法:DDA算法,中点画线法、Bresenham法。
- 圆和圆弧的生成算法:DDA算法,中点画线法,Bresenham法
- 线宽生成算法:刷子绘制法,实区域填充法
- 线型的处理
- 区域填充法:扫描线法,边填充法,种子填充法,扫描线种子填充法,
- 反走样技术:像素细分技术,Bresenham反走样技术
- 曲线生成:Bezier曲线和B样条曲线,包括二阶、三阶曲线等。
- 图形变化:平移、缩放、旋转
- 坐标系之间的变换:局部坐标、世界坐标、摄像机坐标、屏幕坐标
- 四边形裁剪算法:Cohen-Sutherland裁剪算法、中点分割裁剪算法、Liang-Barskey裁剪算法
- 多边形裁剪算法:Sutherland-Hodgman算法,Weiler-Atherton算法
- 三维线段裁剪算法:长方体裁剪算法,视椎体裁剪算法
- 图形消隐:背面剔除算法,画家算法,Weiler-Atherton算法,BSP树算法、深度缓冲区算法,Warnock算法
- 曲面的生成:Bezier曲面的生成,B样条曲面的生成,特别是二阶和三阶曲面
- 地形的生成算法
- 雨雪的模拟算法
第1章 绪论
什么是计算机图形学?
计算机图形学是研究通过计算机将数据转化为图形,并在专门显示设备上显示的原理、方法和技术的学科。也就是如何用计算机生成、处理和显示图形的一门学科。
计算机图形学是研究怎样利用计算机来生成、处理和显示图形的原理、方法和技术的学科。
计算机图形学的应用
- 图形用户接口 (2) 工业应用 (3) 商业领域 (4) 艺术领域 (5) 科学计算可视化 (6) 虚拟现实 (7) 系统环境模拟
图形和图像的区别
- 表示方法不同:图形是由基本几何体(直线,点,圆、曲线、三角形等)构成的实体,同时具有几何属性和视觉属性。图像是由很多像素点构成的点阵信息。
- 生成方法不同:图形是通过计算机算法生成的,而图像是通过照相机,摄像机等扫描设备或图像生成软件制作而成。
- 研究侧重点不同:图形学主要研究如何使用计算机表示几何体,构建几何模型、如何通过建立数学模型或者算法把真实的或者想象的物体显示出来。图像处理主要研究如何将一种图像处理成另一种图像,包括图像增强、复原、解析和理解、编码、压缩、匹配,识别等。
第2章 计算机图像处理及显示的基本原理
显卡工作流程
- 通过数据总线将要显示的图形或者图像数据送入GPU(图形处理器)。
- GPU对送入的数据进行处理然后送入帧缓冲器(或称显存) 。
- 送入帧缓冲器中的数据将被送入视频控制器。视频控制器将根据接口的类型确定处理方式,完成数模转换;
- 视频控制器的输出将送到显示屏。
概念
帧缓存/显存:显存用来存储屏幕上像素的颜色值。帧缓冲器中的单元数目与显示器上的像素数目相同,单元与像素一一对应,各单元的数值决定了其对应的像素的颜色。(比如一个像素24位)
显卡分辨率:显卡分辨率是指显卡输出给显示器并能在显示器上描绘的像素点的数量。
显卡颜色深度:每个像素包含三种颜色:R,G,B。像素的精细度由组成像素的颜色的位数和照射到像素的颜色的强度决定。显示透明度,往往还增加8bits来表示透明度。
规定以左手定则根据顶点的排列顺序来确定三角面的朝向。
GPU处理输入的图形数据(渲染流水线)
- 输入装配阶段。从内存中读入相关的顶点和索引,从而生成几何图形的基本要素(点,线以及三角面)。
- 顶点着色阶段。完成顶点转换(从局部坐标系转换到齐次裁剪坐标系中),光照(纹理)等各种形式的运算。
- 曲面细分阶段。将一个大的三角形分解成若干个小的三角形。
- 几何着色阶段。对输入的点进行筛选,然后输出相应的构成几何图形的基本要素。同时几何着色可以输出一系列的点到内存空间中。
- 裁剪。将区域之外的物体去除掉,只显示区域之内的物体。
- 光栅化阶段。将几何图元变为二维图像。第一部分工作:决定窗口坐标中的哪些整型栅格区域被基本图元占用;第二部分工作:分配一个颜色值和一个深度值到各个区域以便进行消隐操作。目的,是找出一个几何单元(比如线段或三角形)所覆盖的像素。
- 像素着色阶段。通过这些点及相应的属性可以在GPU中计算除相应像素的颜色,光照的影响,阴影等处理效果。
- 输出融合阶段。一些像素无法通过深度测试而被排除,而另一些像素送入,与此前已经写入到后台缓冲区中的像素进行相应的融合处理。
第3章 基本图形生成 ★
画线算法
数值微分画线法(DDA)
- 输入\(P_0(x_0,y_0), P_1(x_1,y_1)\)
- 计算增量 $ x=,y= \ ((y_1-y_0),(x_1-x_0))$
- 循环\(Length\)次,\(x_{i+1} = x_i+\Delta x, y_{i+1} = y_i+\Delta y\),每步结果对不是整数那个四舍五入

中点画线法
原理:\(d = 2F(x_k+1,y_k+0.5) = 2a(x_k+1)+2b(y_k+0.5) + c, d_0 = 2a+b\)
输入\(P_0(x_0,y_0), P_1(x_1,y_1)\)
\(a=y_0-y_1, b=x_1-x_0\)
\(d = 2a+b\), \(delta1 = 2a , delta2 = 2(a+b)\)
当\(d\ge 0\),取下点 y不变 \(y_{i+1} = y_i\), \(d+=delta1\);(
x++一直自增)当\(d<0\),取上点 y加一 \(y_{i+1} = y_i+1\), \(d+=delta2\).

Bresenham 画线算法
输入\(P_0(x_0,y_0), P_1(x_1,y_1)\)
\(e=2\Delta y-\Delta x\)
当\(e\ge 0\),取上点 \(y_{i+1} = y_i+1\), \(e'=e+2\Delta y - 2\Delta x\);
当\(e<0\),取下点 \(y_{i+1} = y_i\), \(e'=e+2\Delta y\).

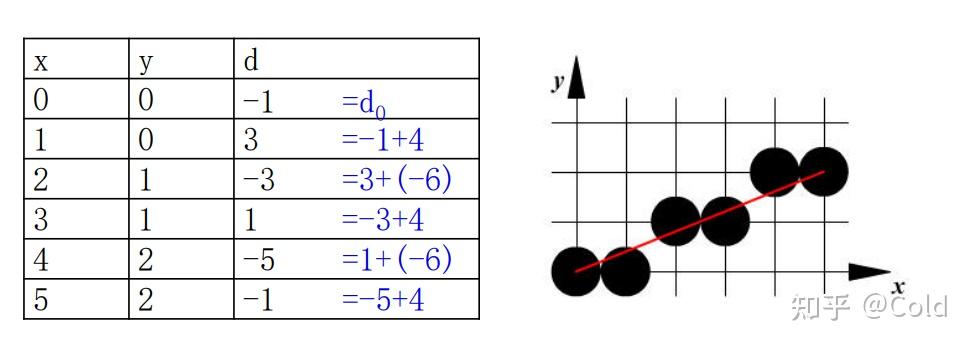
圆形算法
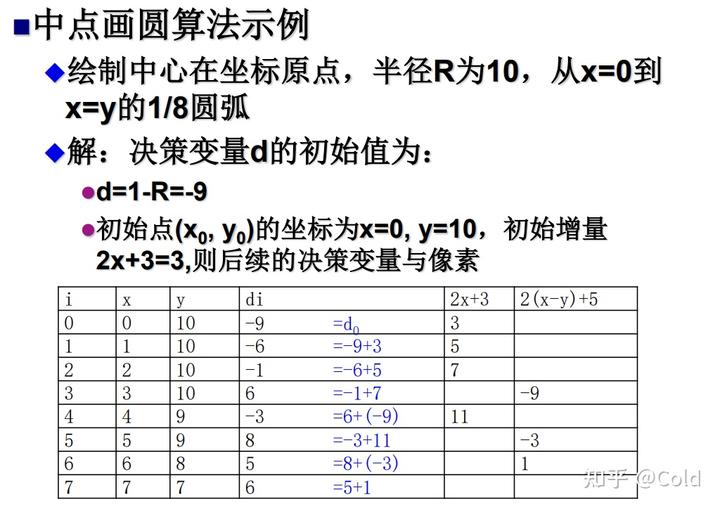
中点画圆算法
基本算法思想就是利用下一个点的绘制要么是右方的点,要么是右下侧的点。
初始值 \(x=0,y=R\),\(d=1-R\)
\(d<0\),y不变,\(d=d+2x+3\)
\(d\ge0\),y减一,\(d= d+2x_n-2y_n+5\)
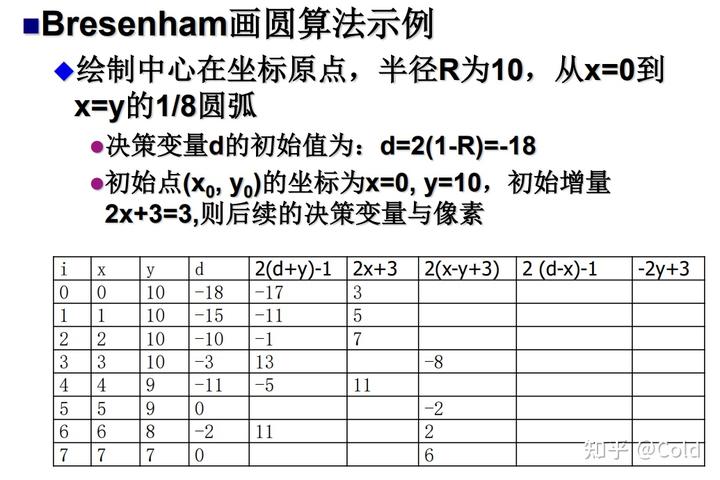
Bresenham画圆算法
利用下一个点的绘制要么是右方的点,要么是右下侧的点,要么是下方的点 不断判定三个距离哪个最短则选择哪个。
- 初始化 x=0, y=R, d=2(1-R)
- d<0, 2(d+y)-1<=0: x=x+1, d=d+2x+3
- d<0, 2(d+y)-1>0: x=x+1, y=y-1, d=d+2(x-y+3)
- d=0: x=x+1, y=y-1, d=d+2(x-y+3)
- d>0, 2(d-x)-1<=0: x=x+1, y=y-1, d=d+2(x-y+3)
- d>0, 2(d-x)-1>0: y=y-1, d=d-2y+3
线宽和线型的处理
- 线宽处理:刷子绘制法,方形刷子绘制法,实区域填充法产生线宽
- 线型处理:看成一个由布尔值对应的像素。每种线型对应一定的长度的像素,每个像素对应相应的布尔值。如果该像素对应的布尔值为1,则绘制该像素。如果对应的布尔值为0,则不绘制该像素。
区域填充
检查某个像素是否在某个多边形区域内
- 转角法:计算点与多边形各个顶点的连线所构成的夹角之和(带方向),为0标明是在区域外;如果为360°标明在区域内。
- 射线法:水平(右)或者垂直(下)方向做射线。判断该射线与多边形交点的个数。交点数为偶数在图形外;交点数奇数在图形内。
扫描线法:
- 求交、排序、两两配对、线段着色
- 注意顶点求交点规则:把所有极值顶点当成两个点
- (活性边表法好像不考?)边表的结构为 \([x,y_{max},\frac1k]\)。 $x: $当前扫描线与活性边的交点, $y_{max}: \(活性边较高端点的\)y$ 坐标值, $1k: $活性边所在直线斜率的倒数。
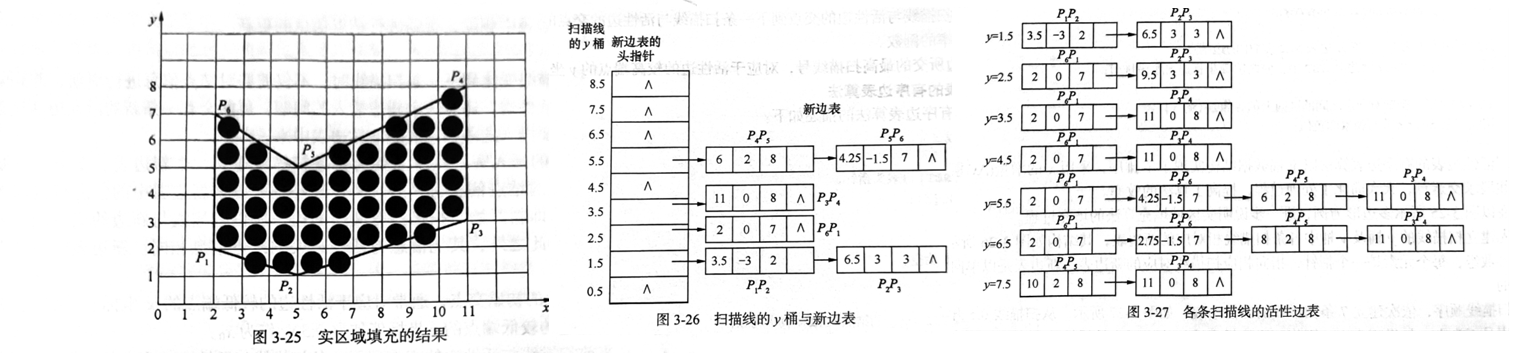
边填充法:该多边形每一条边右边区域像素的颜色全部取补
栅栏填充法:该多边形每一条边与栅栏之间像素的颜色全部取补
种子填充法:四连通/八联通,从某个像素点开始BFS/DFS整某个像素点开始个区域(缺点:堆栈大量使用)
扫描线种子填充法:
- 栈顶像素出栈。
- 沿扫描线对出栈像素的左右像素进行填充,直到遇到边界像素xl和xr为止
- 在区间[xl,xr]中检查与当前扫描线相邻的上下两条扫描线,则把每个 非边界、未填充 的 像素区间的最右像素取为种子像素入栈。
图形反走样技术
问题:阶梯状边界;图形细节失真;狭小图形遗失:动画序列中时隐时现,产生闪烁。本质是用离散的像素去表示连续图形,从而引起失真。
Bresenham区域反走样技术:将多边形每条边与具有一定面积的像素相交的面积大小分为8个等级。相交面积 0-1/8 1/8-2/8……
\(S=(y_{i+1}+ y_i)/2=(y_i+ y_i+m)/2= y_i+m/2=e+m/2\)
### 曲线生成
要求:
- 唯一性
- 几何不变性:用相同的方法去拟合平面空间中不同坐标系下相同的几个点,得到的拟合曲线不变。直角坐标系不具备几何不变性。
- 易于定界:矢量坐标系中\(p(t)=[x(t),y(t),z(t)]\),由于每一个变量都用统一的t标量来描述,非常容易确定其边界。
- 统一性:可以在不增加其他参数的情况下进行维数的扩充。P(t) = [x(t) y(t)] => P(t) = [x(t) y(t) z(t)]
参数样条曲线
- 零阶几何连续性:\(G^0\)连续性,首尾相接
- 一阶几何连续性:\(G^1\)连续性,首尾相接,且切矢量方向连续(一阶导数成比例)
- 一阶几何连续性:\(G^2\)连续性,首尾相接,一二阶导数成比例,曲率连续。

参数样条曲线数学表示:
\[ P(t)=\begin{bmatrix}x(t)\\y(t)\\z(t)\end{bmatrix}=\begin{bmatrix}x_0&x_1&\cdots&x_n\\y_0&y_1&\cdots&y_n\\z_0&z_1&\cdots&z_n\end{bmatrix}\begin{bmatrix}1 \\ \vdots\\t^n\end{bmatrix}=C\cdot T\quad t\in[0,1] \]
Hermite插值样条:已知每个型值点的位置矢量及其切矢量,然后绘制出的样条曲线。
Bezier曲线的生成
Bezier曲线通过控制点来控制曲线的形状。把相邻的点连接起来形成一个特征多边形,并将其作为曲线的轮廓线,然后在每个特征多边形顶点配以伯恩斯坦(Bernstein)多项式作为权函数,对特征多边形的各顶点进行加权求和。 \[ \begin{aligned}&P(t)=\sum_{i=0}^nP_i\cdot BEZ_{i,n}(t)\quad t\in[0,1]\\\\&BEZ_{i,n}(t)=C_n^it^i(1-t)^{n-i},\quad t\in[0,1]\end{aligned} \] De Casteljau算法:递归法绘制点
用直线连接所有相邻的n个控制点,得到其特征多边形。
如果t∈[0,1],则在特征多边形的每一条边上按照t:(1-t)的比例寻找一组新的点,构成新的多边形,该多边形的边比前面的多边形少一条边。
在新的多边形上,重复(2)的操作得到一组新的多边形。在n次这种操作之后,将得到一个点,该点即为曲线上的点。
B样条曲线的生成
B样条曲线由n+m+1个控制点构成,其中\(P_0~ P_n\)这个n+1个控制点控制其第一段曲线, \(P_1~ P_{n+1}\)这个n+1个控制点控制其第二段曲线,…,依次类推,总共m+1段曲线构成B样条曲线。 \[ P(t)=\sum_{i=0}^nP_i\cdot B_{i,n}(t) t\in[0,1] \\ B_{i,n}(t){=}\color{red}\frac1{n!}\sum_{j=0}^{n-i}(-1)^jC_{n+1}^j(t+n-k-j)^n \]
其第i段曲线可表示为:\(\begin{aligned}\mathsf{P}_{i,n}(t)&=\sum_{\mathrm{k=0}}^nP_{i+\mathrm{k}}\cdot B_{k,n}(t)&&t\in[0,1]\end{aligned}\)
第4章 图形变换与裁剪 ★
图形矩阵变换
注:课程默认使用行向量表达,复合变换矩阵要写在行向量的右侧(从左向右结合) $$ T_{3D}= \[\begin{bmatrix}1&0&0&0\\0&1&0&0\\0&0&1&0\\b_x&b_y&b_z&1\end{bmatrix}\] S_{3D}= \[\begin{bmatrix}s_x&0&0&0\\0&s_y&0&0\\0&0&s_z&0\\0&0&0&1\end{bmatrix}\]\
{}={}=_{}=$$
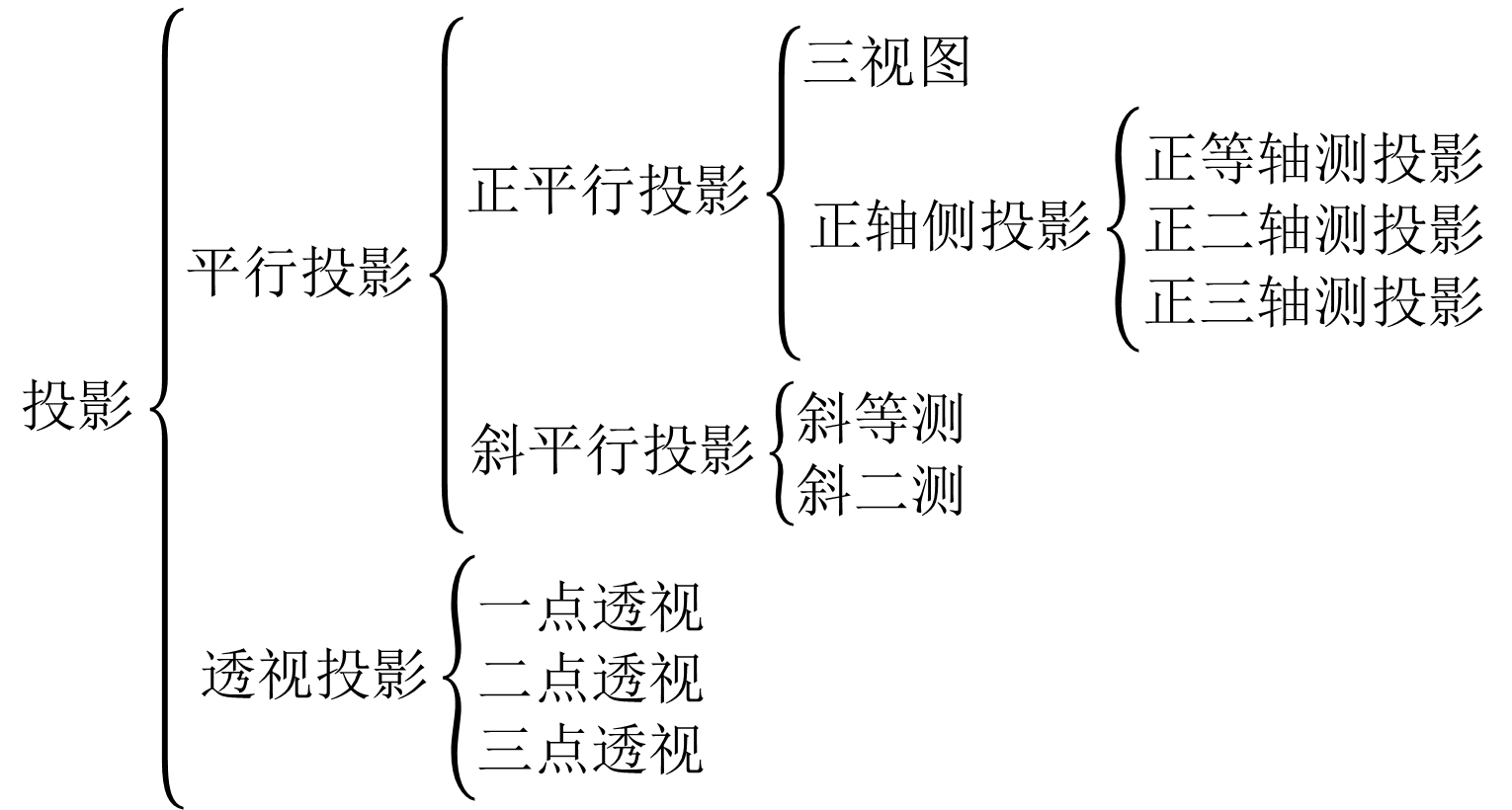
平行投影
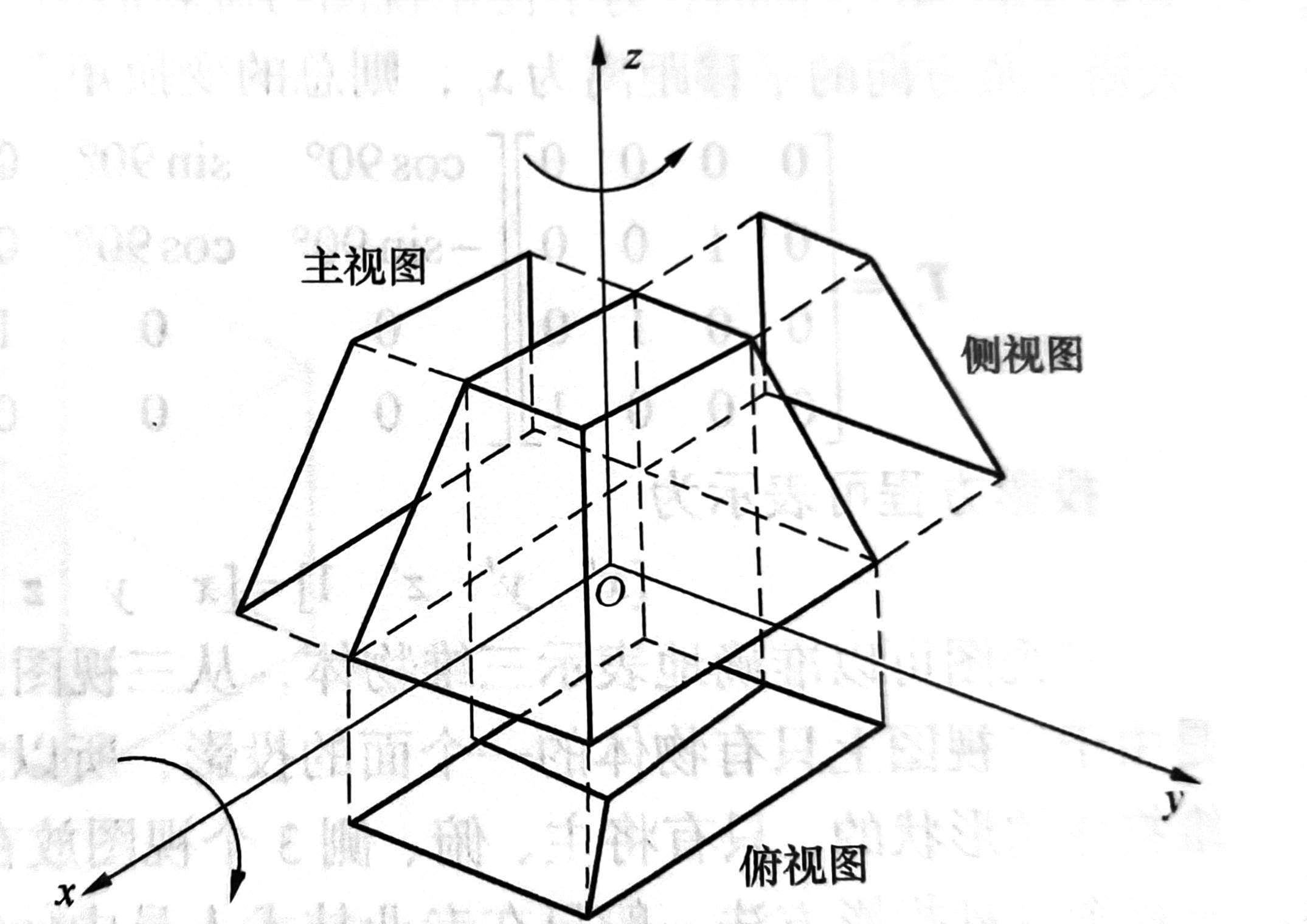
投影平面为xOz面
主视图:y拍扁 \[
T_\nu=\begin{bmatrix}1&0&0&0\\0&0&0&0\\0&0&1&0\\0&0&0&1\end{bmatrix}
\]
俯视图:z拍扁,绕X轴顺时针旋转90度,然后沿Z方向平移一段距离。
\[
T_h=\begin{bmatrix}1&0&0&0\\0&1&0&0\\0&0&0&0\\0&0&0&1\end{bmatrix}\begin{bmatrix}1&0&0&0\\0&\cos(-90^\circ)&\sin(-90^\circ)&0\\0&-\sin(-90^\circ)&\cos(-90^\circ)&0\\0&0&0&1\end{bmatrix}\begin{bmatrix}1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&-z_p&1\end{bmatrix}
\]
侧视图:x拍扁,绕Z轴逆时针旋转90度到xOz面,然后在X轴方向上移动一定距离。
\[
T_W=\begin{bmatrix}0&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{bmatrix}\begin{bmatrix}\cos90^\circ&\sin90^\circ&0&0\\-\sin90^\circ&\cos90^\circ&0&0\\0&0&1&0\\0&0&0&1\end{bmatrix}\begin{bmatrix}1&0&0&0\\0&1&0&0\\0&0&1&0\\-x_L&0&0&1\end{bmatrix}
\]
正轴测投影:将物体绕Z轴逆时针旋转某个角度(比如β角),然后再绕X轴顺时针旋转α角,然后再向xOz面做正平行投影。 \[ R_{zx}=R_zR_x=\begin{bmatrix}\cos \beta & \sin \beta & 0 & 0 \\ -\sin \beta & \cos \beta & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1\end{bmatrix} \begin{bmatrix}1&0&0&0\\0&\cos\alpha&\sin\alpha&0\\0&-\sin\alpha&\cos\alpha&0\\0&0&0&1\end{bmatrix}\begin{bmatrix}1&0&0&0\\0&0&0&0\\0&0&1&0\\0&0&0&1\end{bmatrix} \]
透视投影
- 一点透视:也称为平行透视。即投影平面与投影对象所在坐标系的一个坐标平面平行。
- 两点透视:也称为成角透视。即投影平面与投影对象所在坐标系的一个坐标轴平行,而与另两个坐标轴成一定角度。
- 三点透视:也称为斜透视。即投影平面与投影对象所在的坐标系的坐标轴均不平行。
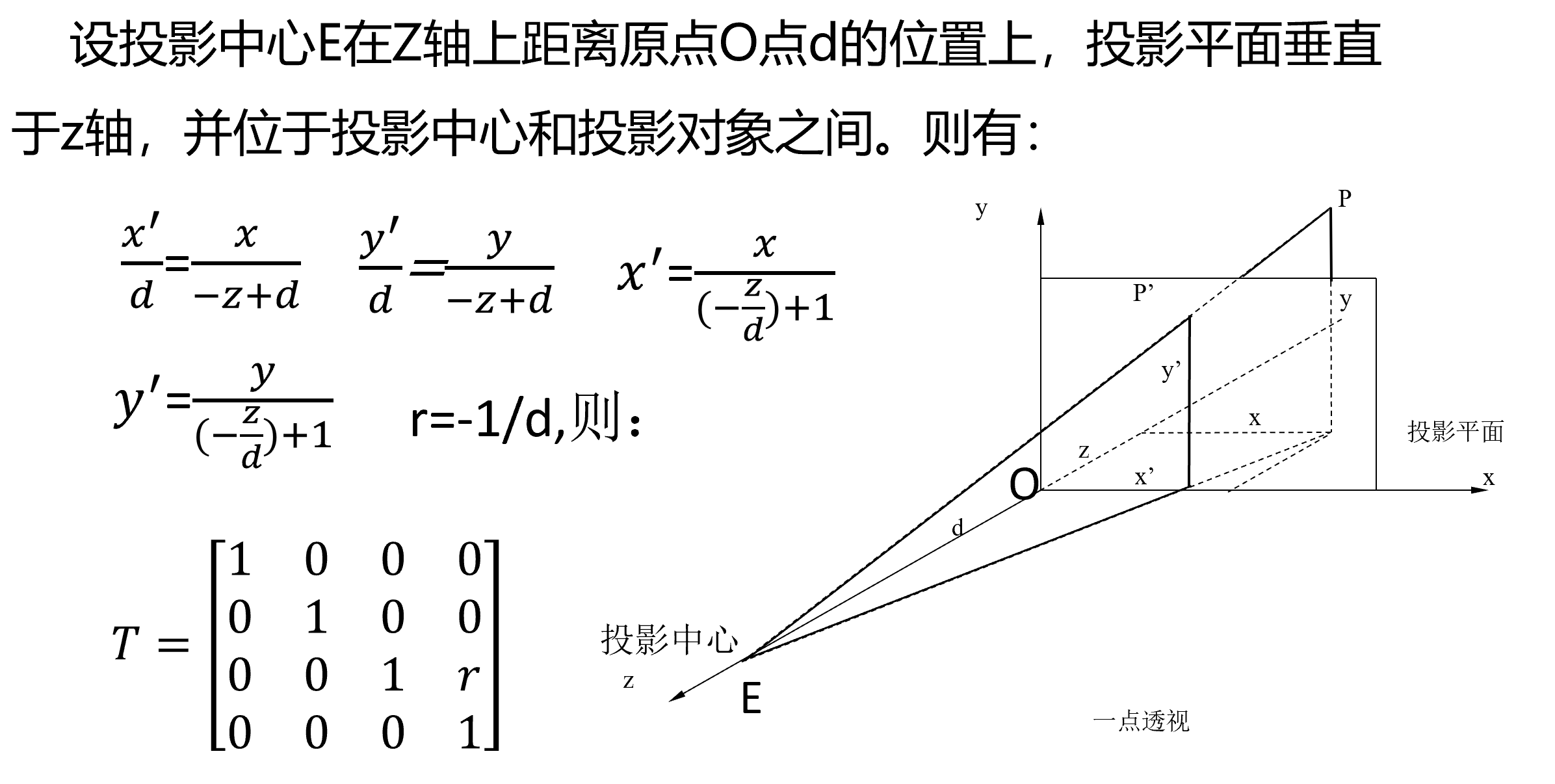
灭点:不平行于投影平面的平行线(如平行于 z 轴的平行线)的投影的汇聚点,这个点称为灭点。(一定落在同一个面上)
主灭点:平行于三维坐标系坐标轴的平行线在投影平面上形成的灭点。
\([x^{\prime},y^{\prime},z^{\prime},1]=[0,0,1/r,1]\) 其对应的投景约矩阵为:
\[ \left[\begin{array}{llll} x^{\prime} & y^{\prime} & z^{\prime} & H \end{array}\right]=\left[\begin{array}{llll} x & y & z & 1 \end{array}\right]\left[\begin{array}{llll} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & q \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right]=\left[\begin{array}{llll} x & y & z & q y+1 \end{array}\right] \] 如果灭点在X轴\([1/p,0,0,1]\)和Y轴\([0,1/q,0,1]\)上,则对应的投影矩阵分别为: \[ P_{x}=\left[\begin{array}{llll} 1 & 0 & 0 & p \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right], P_{y}=\left[\begin{array}{llll} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & q \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right] \]
图形裁剪
Cohen-Sutherland裁剪算法(编码裁剪算法)
- 对线段端点编码,定义为它所在区域的编码;
- 快速判断“完全可见”,若两端点编码均为0,则完全可见。RC0=0且RC1=0
- 快速判断“完全不可见”,线段两端点编码的逻辑位“与”运算结果非零,则完全不可见。RC0&RC1≠0说明直线段位于窗外的同一侧
- 若2)、3)不满足,逐个端点判断其编码 CtCbCrCl(C3C2C1C0) 中位是否为“1”,若是,则需求交,交点的x坐标进行排序,从而将原始线段分割成最多五段线段(四个交点)。然后根据(1)(2)步判断这些线段是否在区域内。
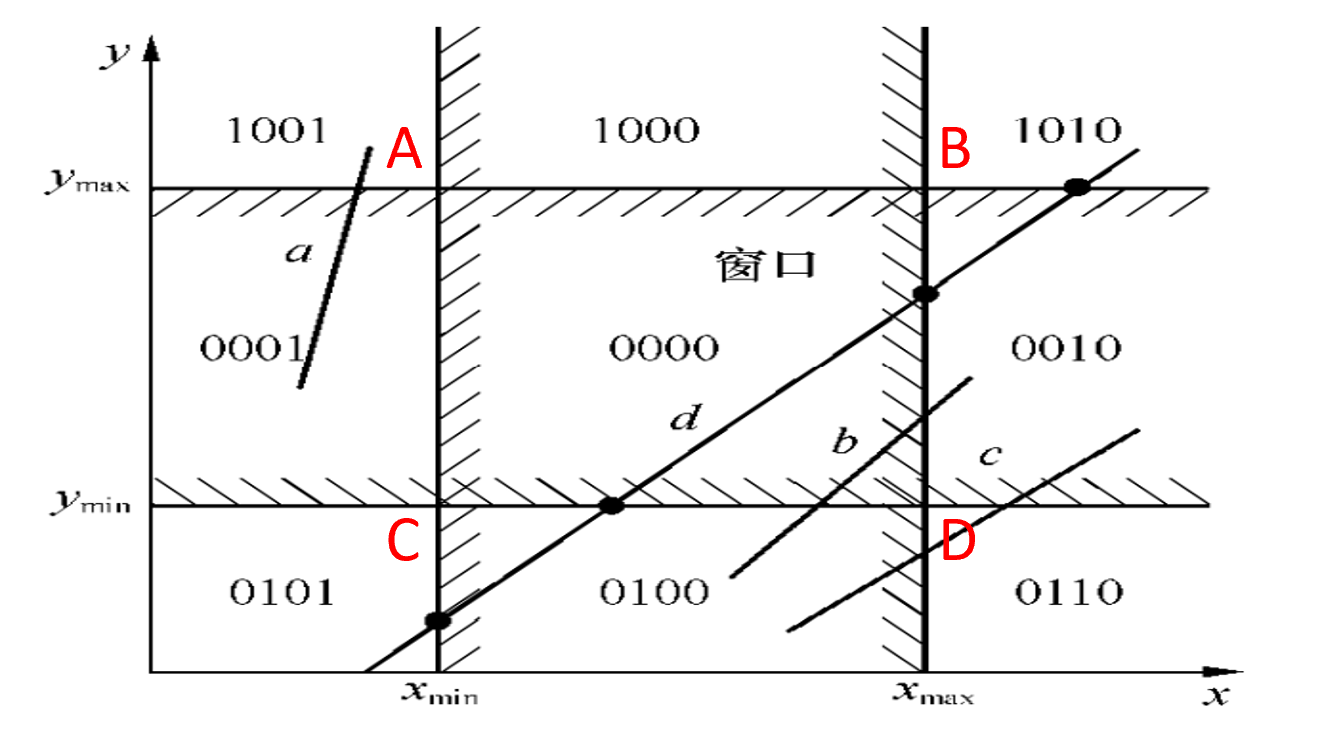
中点分割裁剪算法
中点分割法的思想是通过不断求线段的中点,并采用Cohen-Sutherland算法可见性判断,然后确定可见区域内的线段。
- 固定 P1,测试 P2是否在窗口内,若是,则 P2 是离 P1 点最远的可见点。否则,将线段 P1P2 对分,求出中点 Pm,编码判断线段 PmP2 是否全部在窗口外,若是,则舍弃PmP2,用 P1Pm代替 P1P2;若不是,则用PmP2代替P1P2。
本质就是固定一个端点求,用二分法求这个端点的最远的可见点。
Liang(梁友栋)-Barsky裁剪算法
无论何种情况下,在裁剪区域之内的线段均为:AB ∩ RS ∩ TU
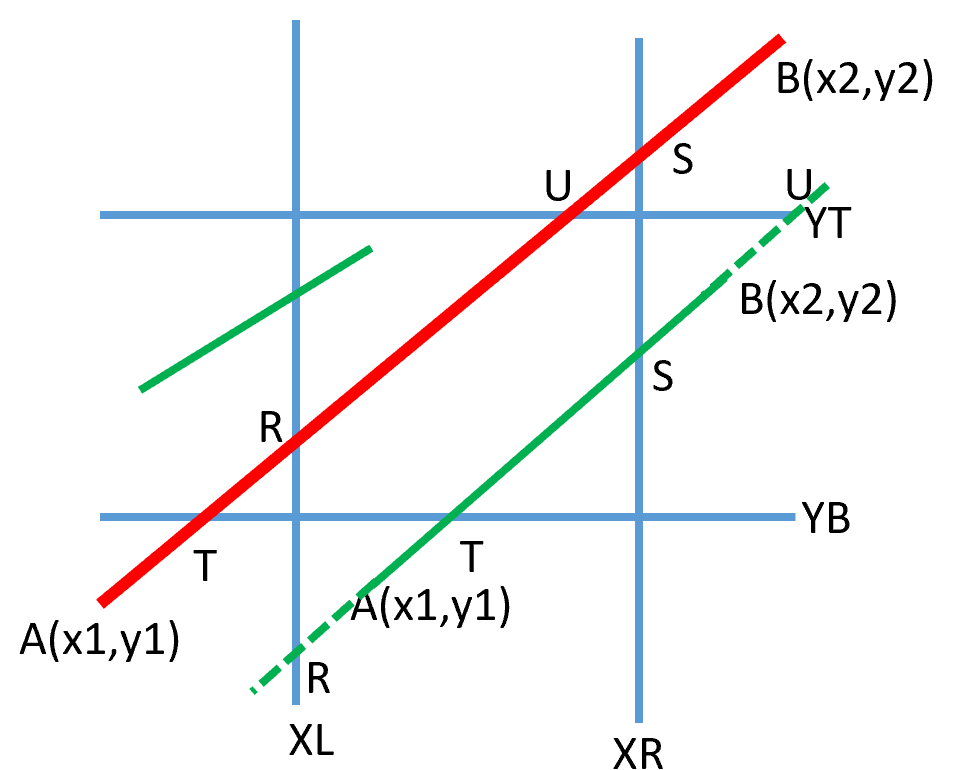
记\(L=\max \left[x_{\min }, \min \left(x_{A}, x_{B}\right)\right], R=\min \left[x_{\max }, \max \left(x_{A}, x_{B}\right)\right]\),不等式若有不成立,则不存在可见线段,不等式为: \[ \left\{\begin{array}{l} L \leqslant R \\ L \leqslant \max \left(x_{T}, x_{U}\right) \\ \min \left(x_{T}, x_{U}\right) \leqslant R \end{array}\right.; \quad \text{斜率>0时} \left\{\begin{array}{l} L \leqslant R \\ L \leqslant x_{U} \\ x_{T} \leqslant R \end{array}\right.; \quad \text{斜率<0时} \left\{\begin{array}{l} L \leqslant R \\ L \leqslant x_{T} \\ x_{U} \leqslant R \end{array}\right. \] A B 斜率大于 0 时,可见线段的端点坐标:\(\begin{array}{l} x_{\alpha}=\max \left(L, x_{T}\right) \\ x_{\beta}=\min \left(R, x_{U}\right) \end{array}\)
A B 斜率小于 0 时,可见线段的端点坐标:\(\begin{array}{l} x_{\alpha}=\max \left(L, x_{U}\right) \\ x_{\beta}=\min \left(R, x_{T}\right) \end{array}\)
多边形裁剪
Sutherland-Hodgman算法
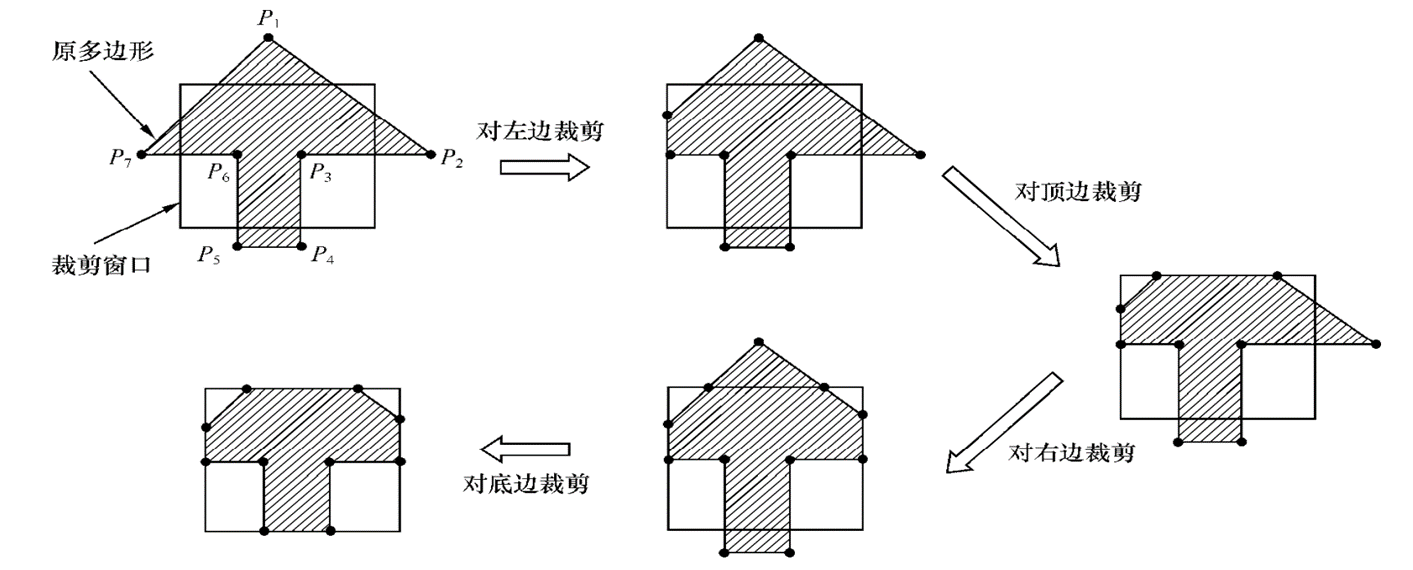
基本思想:用裁剪窗口的每一条边去裁剪某个多边形
- 边 \(P_i P_{i+1}\)
可见一侧,输出\(P_{i+1}\)。
- 边\(P_i P_{i+1}\)不可见一侧,此时没有新的顶点输出。
- 边\(P_i P_{i+1}\)离开窗口,输出交点。
- 边\(P_i P_{i+1}\)进入窗口,该交点和顶点\(P_{i+1}\)都输出。
问题:裁剪凹多边形可能会出现多余的边
Weiler-Atherton算法
可适用于任意类型的多边形,包括有空洞的。将裁剪多边形称为CP,被裁剪多边形称为SP。
- 算法首先将CP和SP的顶点按照外部边界取顺时针,内部边界取逆时针的的方式将其构成环形链表。
- 求出SP与CP边线的所有交点,并将这些交点插入到SP和CP的环形链表中,并标明交点是出点还是进点。
- 算法从任意一个进点开始沿着SP的边线按照边线所标示的方向搜集顶点序列,当遇到出点时,则沿着CP的边线所标示的方向搜集顶点序列,当遇到进点时,则沿着SP的边线所标示的方向搜集顶点序列。
搜索所有点。
图形消隐
背面剔除算法
在取景变换(将物体从世界坐标系转换到摄像机坐标系)之前,将那些背离视点方向而不可见的景物表面剔除。
- 计算多边形的法向向量N和视线向量V。
- 计算法向向量N和视线向量V的夹角θ的余弦Cosθ=N.V。
- cosθ<0,即θ>90°, 则该多边形表面为背面,是不可见的
画家算法
将多边形按照离视点的远近进行排序(P221 判断遮挡,分割),然后先画出被遮挡的多边形,再画出不被遮挡的多边形,用后画的多边形覆盖先画的多边形,从而达到自动消隐的目的。
Weiler-Atherton算法
算法思想:采用裁剪算法的思想对隐藏面进行消隐。
算法步骤如下:
- 先进行初步的深度预排序,即将变换到屏幕坐标系中的景物表面多边形按各顶点的 z 最小值进行排序,形成景物多边形表。
- 以当前具有最大 z 值(即离视点最近)的景物表面作为裁剪多边形 CP 。
- 用CP对景物多边形表中排在后面的景物表面进行裁剪,产生内部多边形 Pin 和外部多边形 Pout 。
- 由于多边形顶点离视点最近的多边形表面不一定是真正排在最前面的可见面,因此,需比较CP与内部多边形 Pin 的深度,检查 CP是否是真正离视点较近的多边形。 如果是,则CP为可见表面,而位于裁剪多边形 CP之内的多边形 Pin 为当前视点的隐藏面,可以消去该隐藏面;如果不是,则选择 Pin 为新的裁剪多边形,重复步骤 3。
- 将位于裁剪多边形之外的景物表面 Pout 组成外裁剪结果多边形表,取表中深度最大即排在最前面的表面为裁剪多边形,重复步骤 3,继续对表中其他景物表面进行裁剪。
- 上述过程递归进行,直到外裁剪结果多边形表为空时为止
BSP树算法
算法思想:平面分割二叉树
先在场景中选取一剖分平面 P1(与视点垂直的平面),将场景空间分割成两个半空间。它相应地把场景中的景物分成两组,相对于视点而言,一组景物多边形位于P1的前面,作为BSP树的左孩子(front),另一组景物多边形位于P1的后面,作为BSP树的右孩子(Back),如果有物体与 P1相交,就将它分割为两个物体分别标识为A和B,再用平面 P2 对所生成的两个子空间继续进行分割,并对每一子空间所含景物进行分类。上述空间剖分和景物分类过程递归进行,直至每一子空间中所含景物少于给定的阈值为止。
优先绘制标识为“back”的子空间中所含的景物,这样可使得前面的物体覆盖后面的物体,从而实现物体的消隐。
深度缓冲区算法
目前大多数的硬件实现方法
算法思想:对投影到显示屏上的每一个像素所对应的多边形表面的深度进行比较,然后取最近表面的属性值作为该像素的属性值。Z缓冲器(Z-buffer,深度缓冲区),深度缓冲器只是帧缓冲器的扩充。
- 将场景中的所有多边形通过取景变换、透视变换变换到屏幕坐标系中,物体的深度比较可通过它们z值的比较来实现。
- 初始化深度缓冲存储器和帧缓冲器。深度缓冲器应初始化为离视点最远的最大z值,帧缓冲器应初始化为背景的属性值。
- 扫描待显示的每一个多边形,比较当前多边形所覆盖的每一个像素点的深度值,如果其深度值比深度缓冲区中当前像素的深度值小,则取代原来的深度值,并将对应像素的属性值保存到帧缓冲区对应的位置中。反之,则不做任何处理。循环该步骤,直到处理完所有的多边形。
Warnock算法
该算法将整个观察范围细分成越来越小的矩形单元,直至每个单元仅包含单个可见面片的投影或不包含任何面片。
单纯窗口:景物已经足够简单,比如没有任何可见物体,或者窗口已被一个可见面片完全充满
算法思想:将非单纯的窗口四等分为4个子窗口(四叉树),对每个子窗口再进一步判别是否是单纯的,直到窗口单纯或窗口边长已缩减至一个像素点为止。
- 对每个窗口进行判断,若画面中所有多边形均与此窗口分离,即此窗口为空,则按背景光强或颜色直接显示而无需继续分割。
- 若窗口中仅包含一个多边形,则窗口内多边形外的区域按背景光强或颜色填充,多边形内按多边形相应的光强或颜色填充。
- 若窗口与一个多边形相交,则窗口内多边形外的区域按背景光强或颜色填充,相交多边形内位于窗口内的部分按多边形相应的光强或颜色填充。
- 若窗口被一个多边形包围且窗口内无其他的多边形,则窗口按此包围多边形相应的光强或颜色填充。
- 若窗口至少被一个多边形包围且此多边形距离视点最近,则窗口按此离视点最近的包围多边形的相应光强或颜色填充。
- 若以上条件都不满足,则继续细分窗口,并重复以上测试。
四元素,看不懂…
第5章 模型生成方法
模型的表示方法
三角面:顶点+索引
参数多项式曲面
\[ \begin{cases}x=x(u,v)\\y=y(u,v)\\z=z(u,v)&\end{cases}\quad(u,v)\in[0,1]\times[0,1] \]
\[ P(u,v)=\sum_{i=0}^m\sum_{j=0}^na_{ij}u^i\nu^j=U^\mathrm{T}AV\quad(u,v)\in[0,1]\times[0,1] \]
Bezier曲面
\[ P(u,v)=\sum_{i=0}^m\sum_{j=0}^nP_{ij}BEZ_{i,m}(u)BEZ_{j,n}(v)\quad u\in[0,1],v\in[0,1]\] $$
B 样条曲面
\[ P(u,v)=\sum_{i=0}^m\sum_{j=0}^nP_{ij}B_{i,k}(u)B_{j,h}(\nu)\quad u\in[0,1],\nu\in[0,1] \]
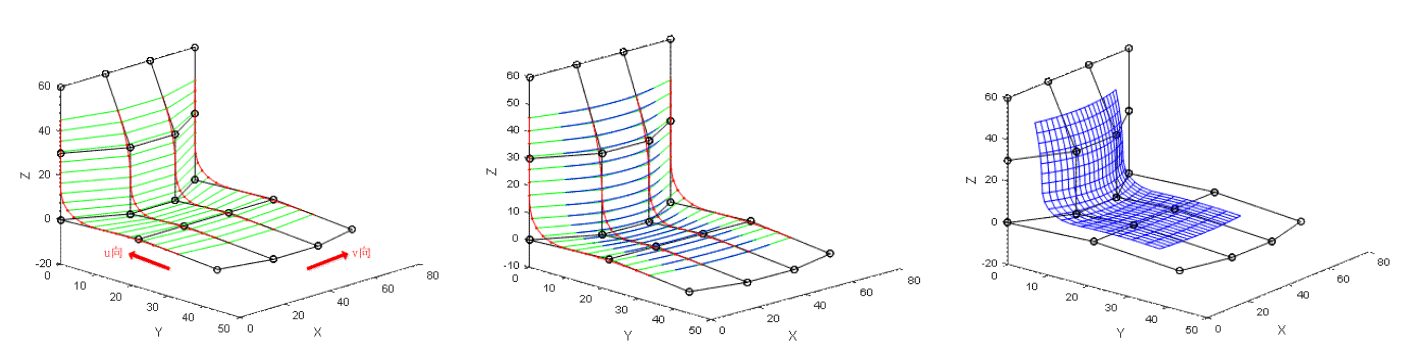
3D地形模拟
Diamond-Square算法
- 给定一个四边形,四个顶点的坐标(包含高度),定义一初始高度因子h和一缩放倍数b。
- 迭代,先求出四边形的中心点高度为顶点平均高度+h*r的随机数,再分别求出4个边的中点,高度为两端点高度的平均值+h*r
- 修正高度因子 h=h/b,用(2)的方法分别对这 4 个小正方形进行处理。直到达到所期望的山形细腻程度。
植物形态模拟
L系统的植物形态模拟
- F:从当前位置向前走h的长度,同时画线
- G:从当前位置向前走h的长度,但不画线
- +:从当前方向向左转δ角度
- −:从当前方向向右转δ角度
- |:原地转向180°
定义一个产生式,通过产生式生成新的符号串。如果进行多次迭代,可生成更长的新的符号串,然后根据所产生的符号串来生成对应的树。

迭代函数算法(Iterated Function System,IFS)
IFS系统由一个压缩仿射变换集\(X=\{w_1,w_2,…,w_N\}\)和对应概率集\(P=\{p_1,p_2,…,p_N\}\)组成 \[ \begin{gathered}\sum_{j=1}^Np_j=1,p_j>0,j=1,2,\cdots,N\\\boldsymbol{w}_j\begin{pmatrix}x\\y\end{pmatrix}=\begin{pmatrix}\boldsymbol{a}_j&\boldsymbol{b}_j\\\boldsymbol{c}_j&\boldsymbol{d}_j\end{pmatrix}\begin{pmatrix}x\\y\end{pmatrix}+\begin{pmatrix}\boldsymbol{e}_j\\\boldsymbol{f}_j\end{pmatrix},\boldsymbol{j}=1,2,\cdots,N\end{gathered} \] 输入:初始点的坐标x,y; 输出:屏幕上显示的树
- 输入N或者设定N为某个固定值, 输入或设置迭代次数M。
- 随机生成N个W概率值,并保存到w[N]。
- 随机生成N个概率值,并保存到P[N]。
- 随机生成概率值p。
- 轮盘选择法。如果P<P[0],则w= w[0]; 反之,如果P<p[0]+P[1],则w= w[0]+w[1];….
- 根据前面的公式更新x,y。
- 在屏幕上(x,y)的位置以一定的亮度或者颜色显示该像素。
- 循环执行步骤(4)~(7)M次。
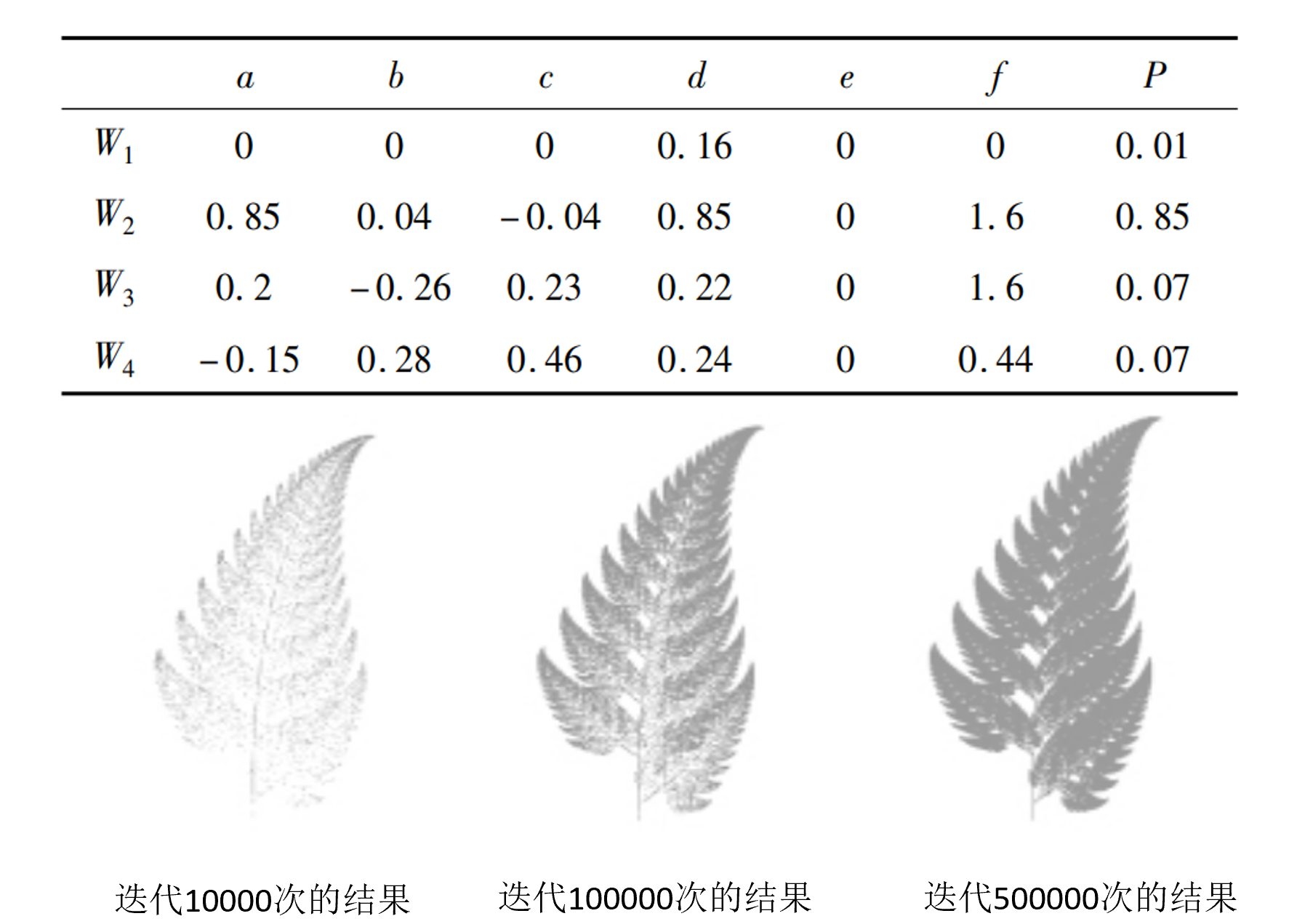
粒子系统:雨雪现象模拟、液态流体模拟
- 生成一定数量的初始粒子,对其各个属性进行赋值。
- 更新粒子的运动参数,比如速度,加速度,位置,生命周期等。
- 针对每一个粒子,在粒子对应的位置上绘制位图,并进行位移的映射,背景融合等。
- 删除已经消亡的粒子,释放其占用的资源。
在模拟时都是在每一帧对其属性进行更新。
- 基于粒子系统的喷泉模拟
- 基于粒子系统的瀑布模拟
气态流体模拟
细胞自动机:又称为元胞自动机(Cellular Automata),是一种在空间和时间上都离散的演化动力系统。每个元胞之上都有若干种离散或者连续的状态,这些状态在每一个时间步都会按照相同的规则发生变化,于是形成了整个元胞自动机的演化过程。
例子:火焰的模拟,\(s_{i,j}^t\)局部温度\(u_{i,j}^t\)燃料供应……
第6章 图形显示技术
光照模型
- 光照模型分类:几何光照模型(局部光照模型和整体光照模型)、物理光照模型
- 光源的分类:点光源、线光源、面光源、体光源
光照基本模型
漫反射光(diffuse Reflection):当光线照射到物体表面,有一部分光线将进入物体内部,部分会被吸收,而另一部分会从内部向各个方向散射并返回表面,这就形成漫反射光。\(\begin{aligned}c_d&=\max(\texttt{L.n, 0})\cdot B_L\otimes m_d\end{aligned}\)
环境光照(Ambient Light):从其他物体发射过来的光线照射到物体所形成的间接光照。\(c_a=A_L\otimes\boldsymbol{m}_d\mid\)
镜面光照(Specular reflection):一部分光将被反射,另一部分光被折,被反射的部分称为镜面反射光,只有观察者在特定的角度才能看到。\(\mathbf{c}_s=\max\left(\mathbf{L}\cdot\mathbf{n},0\right)\cdot\mathbf{B}_L\otimes\mathbf{R}_F(\alpha_h)\frac{m+8}8{\left(\mathbf{n}\cdot\mathbf{h}\right)}^m\)
光照整体模型: \[ \begin{aligned} \text{LitColor}& =\mathbf{c}_a+\mathbf{c}_d+\mathbf{c}_s \\ &=\mathbf{A}_L\otimes\mathbf{m}_d+\max\left(\mathbf{L}\cdot\mathbf{n},0\right)\cdot\mathbf{B}_L\otimes\left(\mathbf{m}_d+\mathbf{R}_F(\alpha_h)\frac{m+8}8{\left(\mathbf{n}\cdot\mathbf{h}\right)}^m\right) \end{aligned} \]
- L:光源的光向量 n: 表面法向 h: 光向量与观察向量之间的中间向量 $A_L: $入射的环境光量。 \(m_d:\)根据表面漫反射率而反射的入射光量。 L.n: 光线与法向量之间夹角的余弦。 \(a_h{:}\) 中间向量h与光向量之间的夹角。 \(R_F(a_h):\) 中间向量h (由表面点指向观察点的单位向量) 所反射到观察者眼中的光量。 m: 控制表面的粗糙度。\((\mathbf{n}\cdot\mathbf{h})^m\)线h与宏观表面法向n之间夹角为\(\Theta h\)的所有为平面片段。 \(\frac{m+8}{s}:\)在镜面发射过程中,为模拟能量守恒所采用的归一化因子。
环境光照
- 环境光模型(物体表面对环境光反射的强度)
- 漫反射模型(观察者从不同角度观察到的反射光具有同样的亮度,这样的反射光成为漫反射光)
- 镜面反射(反射光 => 对入射光的直接反射)
- Phong模型(环境光 + 漫反射光 + 镜面反射光)
整体光照模型:光线追踪
明暗处理
Gouraud明暗处理
基本思想:对离散的顶点颜色采样进行双线性插值得到内部点颜色。
- 计算每个多边形顶点的平均单位法矢量
- 对每个顶点根据简单光照模型计算光强
- 在多边形表面上对顶点颜色进行线性插值
特点:(1)只适用于简单的漫反射模型(2)线性光强度插值会引起马赫带效应
Phong明暗处理
- 计算多边形顶点处曲面法向矢量的平均值。
- 对离散的多边形顶点法向量进行双线性插值,得到面上每个点的法向矢量。
- 按光照模型确定多边形内部各点的光强
纹理细节模拟
颜色纹理:将图片映射到物体表面的方式来实现。将图片的四个角点的坐标分别定义为(0,0) (0,1) (1,1) (1,0)。三角形每一个顶点均对应图片的一个(u,v)坐标。
几何纹理:物体表面的微观几何形状(粗燥程度)。物体表面法向量矢量的修改可通过在各采样点的位置上增加一个扰动函数,对其做微小的扰动,从而改变表面的微观几何现状来实现。
过程纹理:通过过程迭代函数生成纹理。目的是用简单的参数来逼真的描述复杂的自然纹理细节。例如:噪声函数,湍流函数等来动态的生成天空,水流等。
复习大纲总结
图形学基本概念
1. 什么是计算机图形学?
研究通过计算机,将数据转化为图形,并在专门显示设备上显示的原理、方法和技术的学科。也就是如何用计算机生成、处理和显示图形的一门学科。
2. 计算机图形学的主要研究内容包括哪些?
硬件部分:包括各种输入/输出、图形处理设备或器件的研究
软件部分:
- 图形生成算法的研究,包括基本图形的生成,比如直线,圆/圆弧,多边形,曲线/曲面,多面体,自然现象/自然景物等。
- 图形变换算法的研究,包括图形在平面或者空间中的变换,各种视窗之间的转换,平面和空间裁剪,消隐等。
- 图形显示技术研究,包括光照、材质、纹理、阴影、透明、光线追踪等技术的研究。
3. 计算机图形学的主要应用领域。
- 图形用户接口 (2) 工业应用 (3) 商业领域 (4) 艺术领域 (5) 科学计算可视化 (6) 虚拟现实 (7) 系统环境模拟
4. 图形和图像的主要区别是什么?
- 表示方法不同:图形是由基本几何体(直线,点,圆、曲线、三角形等)构成的实体,同时具有几何属性和视觉属性。图像是由很多像素点构成的点阵信息。
- 生成方法不同:图形是通过计算机算法生成的,而图像是通过照相机,摄像机等扫描设备或图像生成软件制作而成。
- 研究侧重点不同:图形学主要研究如何使用计算机表示几何体,构建几何模型、如何通过建立数学模型或者算法把真实的或者想象的物体显示出来。图像处理主要研究如何将一种图像处理成另一种图像,包括图像增强、复原、解析和理解、编码、压缩、匹配,识别等。
5. 计算机图形处理系统的主要构成。
典型的计算机图形系统包括 处理、存储、交互、输入、输出 5个基本功能
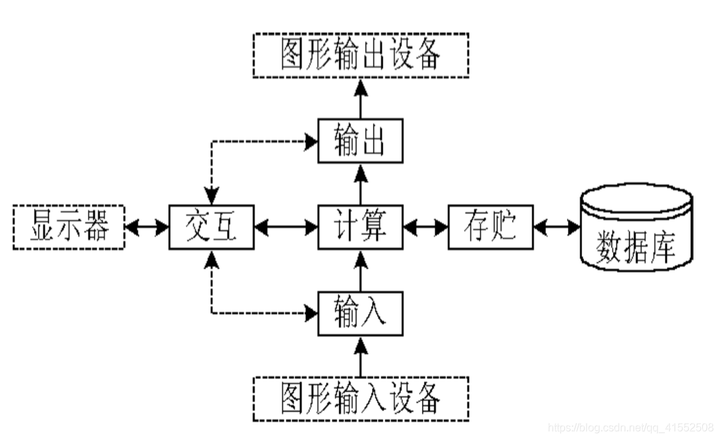
6. 显卡的工作流程。
图像或者图形数据在CPU处理后,通过下面四个步骤到达显示器:
- 通过数据总线将要显示的图形或者图像数据送入GPU(图形处理器)。
- GPU对送入的数据进行处理然后送入帧缓冲器(或称显存) 。
- 送入帧缓冲器中的数据将被送入视频控制器。视频控制器将根据接口的类型确定处理方式,完成数模转换;
- 视频控制器的输出将送到显示屏。
7. 什么是显示存储器?
显存用来存储屏幕上像素的颜色值,简称帧缓冲器,俗称显存。帧缓冲器中的单元数目与显示器上的像素数目相同,单元与像素一一对应,各单元的数值决定了其对应的像素的颜色。
8. GPU的基本概念。
GPU是专为执行复杂的数学和几何计算而设计的微处理器,能够将复杂的图形转换成显示器能够显示的图像。GPU可通过编程完成所需要的图形变换和计算。
GPU可以完成大量的并行计算。由很多的流处理单元(SM,streaming multiprocessor)构成,每一个流处理单元由多个核(计算单元),任务调度器,寄存器组,指令缓冲器,纹理缓冲区,纹理映射单元等构成。
9. 显卡分辨率的含义。
显卡分辨率是指显卡输出给显示器并能在显示器上描绘的像素点的数量。分辨率越大,所能显示的图像的像素点就越多,并且能显示更多的细节,当然也就越清晰。
显卡分辨率跟显存的大小以及视频控制器上RAM DAC的速率有关。如果显存足够大,则RAM DAC决定了分辨率的最大值。
10. GPU堆包含哪几种主要的类型,具有什么样的特点?
- 上传堆:CPU只能将数据传送给上传堆,上传堆不能向CPU传数据。
- 默认堆:默认堆需要通过上传堆传送数据,CPU不能直接访问。
- 回读堆:GPU可通过回读堆将数据传送给CPU。
11. GPU渲染流水线包含哪几个阶段,分别完成什么任务?
- 输入装配阶段。从内存中读入相关的顶点和索引,从而生成几何图形的基本要素(点,线以及三角面)。
- 顶点着色阶段。完成顶点转换(从局部坐标系转换到齐次裁剪坐标系中),光照(纹理)等各种形式的运算。
- 曲面细分阶段。将一个大的三角形分解成若干个小的三角形。
- 几何着色阶段。对输入的点进行筛选,然后输出相应的构成几何图形的基本要素。
- 裁剪。将区域之外的物体去除掉,只显示区域之内的物体。
- 光栅化阶段。将几何图元变为二维图像。
- 像素着色阶段。通过这些点及相应的属性可以在GPU中计算除相应像素的颜色,光照的影响,阴影等处理效果。
- 输出融合阶段。一些像素无法通过深度测试而被排除,而另一些像素送入,与此前已经写入到后台缓冲区中的像素进行相应的融合处理。
12. 光照的基本原理
当光照射到物体表面时,物体将吸收一部分光,同时也会反射或透射一部分光。反射或透射出的光进入人的眼睛所显示出的颜色就是物体的颜色。
13. 光照模型的分类
- 几何光照模型:以几何学原理为基础,形式简单,精度低,主要用于图像渲染。
- 局部光照模型:局部光照模型假设物体表面不透明,反射均匀,光源直射物体表面,可模拟漫反射,镜面反射,阴影等。
- 整体光照模型:在模拟局部光照模型的基础上,还须考虑周围环境对景物表面的影响。可以模拟镜面映像,透明,折射,相邻景物之间的色彩辉映等较为精致的光照效果。
- 物理光照模型:以电池波反射理论为基础,精度高,形式比较复杂,用于光谱分析等物理领域。
14. 光源的分类
- 点光源:光线由中心点均匀向四周散射。在光源比场景中的物体小得多或者距离物体足够远时,可将该光源视为点光源。
- 线光源:发光的光源呈一条直线则称为线光源。线光源可看成由无数个点光源构成。比如日光灯,穿过单缝的光等。
- 面光源:面光源是一种通过将光源均匀分布在一个平面上实现整体均匀照明效果的照明装置。
- 体光源:体光源在所有方向上发射光线,产生全方位的光照效果。
15. 纹理的表现形式。
- 颜色纹理:将图片映射到物体表面的方式来实现。
- 几何纹理:物体表面的微观几何形状(粗燥程度)。
- 过程纹理:过程纹理用于表现各种规则或不规则的动态变化的自然景象。
16. 纹理的过滤方式及寻址方式
- 纹理过滤:纹理图与实际待显示的图形大小不一致的情况,需要通过纹理过滤来解决。
- 点过滤:在纹理贴图时,选择与待投影到屏幕上的几何体分辨率最为匹配的Mipmap层级,并根据具体需求选用常数插值或线性插值。
- 线性过滤:在纹理贴图时,选区与待投影到屏幕上的几何体分辨率最为匹配的两个临近的Mipmap层级(一个稍大于屏幕上几何体的分辨率,一个稍小于屏幕上几何体的分辨率),然后对这两种MipMap层级的图分别进行常量过滤或线性过滤,生成他们各自相应的纹理颜色。最后再在这两种插值纹理之间进行颜色的插值计算。
- 各向异性过滤:需要对映射点周围8个(正方体)或更多的像素进行取样,获得平均值后映射到像素点上。
- 寻址模式:当设定的纹理坐标值大于(1.0.1.0)时,则通过寻址模式来解决。
- 重复寻址模式(Wrap):通过在坐标的每个整数点处重复绘制图像来托充纹理函数。
- 边框颜色寻址模式:通过将每个不在 [0,1] 范围内的坐标(u,v)都映射为指定的颜色(边框颜色)而拓充纹理函数
- 钳位寻址模式:通过将范围[0,1]外的颜色使用边缘的纹理坐标内容进行延伸
- 镜像寻址模式:通过在坐标的每个整数点处绘制图像的镜像来扩充纹理函数。
17. 多级纹理的基本原理
多级纹理是指使用多个不同大小的纹理图片作为贴图来提高画面质量的方法。针对物体处于不同的距离,采用不同分辨率大小的纹理贴图,可以提高图像显示质量,降低图像渲染的复杂度。
18. 模型的表示方法
- 通过三角形、四边形、曲面方程等来模拟物体的表面,最后形成三维模型;
- 是通过无数个细小的四面体、球体等基本几何体来构成整个物体。
19. Direct3D 12图形绘制的基本原理
CPU的数据传递给GPU之后,GPU将把它保存到到GPU的存储空间中。Direct12版本将其分成上传堆、默认堆和回读堆,并用于存储不同类型的图形数据,同时通过不同的API对其进行操作。Direct3D提供的图形接口,通过与GPU卡的通信及编程实现对图形的计算和显示。其原来由CPU进行的计算则转移到GPU中,由GPU计算出对应的像素位置,然后再进行显示。
20. 三维模型顶点的数据结构表示
struct Vertex{
XMFLOAT3 Pos; //顶点的坐标
XMFLOAT4 Color; //顶点的颜色,第四个位置表示alpha通道,用于控制颜色的透明度
};
std::vector<Vertex> Vertices; //存储所有的顶点
std::vector<int> Indices32; //存储所有三角面对应顶点的索引
// 一个正方体
Vertices[0].Pos=XMFLOAT3(-1.0f, -1.0f, -1.0f);
Vertices[1].Pos=XMFLOAT3(-1.0f, +1.0f, -1.0f);
Vertices[2].Pos=XMFLOAT3(+1.0f, +1.0f, -1.0f);
Vertices[3].Pos=XMFLOAT3(+1.0f, -1.0f, -1.0f);
Vertices[4].Pos=XMFLOAT3(-1.0f, -1.0f, +1.0f);
Vertices[5].Pos=XMFLOAT3(-1.0f, +1.0f, +1.0f);
Vertices[6].Pos=XMFLOAT3(+1.0f, +1.0f, +1.0f);
Vertices[7].Pos=XMFLOAT3(+1.0f, -1.0f, +1.0f);
Indices[0]=0;
Indices[1]=1;
Indices[2]=2; //左手定则来确定其法向
Indices[3]=0;
Indices[4]=2;
Indices[5]=3; // 左手定则来确定其法向
……图形学基本算法
要求:算法的基本原理,算法描述,算法执行过程分析,过程计算,编程实现等。
1. 直线生成算法:DDA算法,中点画线法、Bresenham法。
DDA略
中点画线法
检验 0 ≤ k ≤ 1
a = y0 - y1, b = x1 - x0
d0 = 2a+b
当\(d\ge 0\),取下点 y不变 \(y_{i+1} = y_i\), \(d'=d+2a\);
当\(d<0\),取上点 y加一 \(y_{i+1} = y_i+1\), \(d'=d+2a+2b\).
Bresenham法
检验 0 ≤ k ≤ 1
\(\Delta y\) = y1 - y0, \(\Delta x\) = x1 - x0
e = \(2\Delta y-\Delta x\),
当\(e\ge 0\),取上点 \(y_{i+1} = y_i+1\), \(e'=e+2\Delta y - 2\Delta x\);
当\(e<0\),取下点 \(y_{i+1} = y_i\), \(e'=e+2\Delta y\).
2. 圆和圆弧的生成算法:DDA算法,中点画线法,Bresenham法
DDA算法
\(y_{n+1}= y_n-εx_n\)
\(x_{n+1}= x_n+εy_n\)
中点画线法
初始值 \(x=0,y=R\), \(d=1-R\)
\(d<0\),y不变,\(d=d+2x+3\)
\(d\ge0\),y减一,\(d= d+2x-2y+5\)
Bresenham法
- 初始化 \(x=0, y=R, d=2(1-R)\)
- d<0, 2(d+y)-1<=0: \(x=x+1, d=d+2x+3\)
- d<0, 2(d+y)-1>0: \(x=x+1, y=y-1, d=d+2x-2y+6\)
- d=0: 同上
- d>0, 2(d-x)-1<=0: 同上
- d>0, 2(d-x)-1>0: \(y=y-1, d=d-2y+3\)
3. 线宽生成算法:刷子绘制法,实区域填充法
刷子绘制法
如果直线斜率小于等于1,则将刷子置成垂直方向。使垂直方向有w个像素。每次在中心点上下绘制w/2个像素。
如果直线斜率大于1,则将刷子支撑水平方向。使水平方向上有w个像素。如右图所示。
缺点: (1) 线宽较大时,不自然 (2)折线处有缺口 (3)宽度不符合要求 (4)对称问题:奇偶数像素,效果不同
方形刷子绘制法:将正方形的中心对准单线条像素,然后沿单线条对应方向移动。
4. 线型的处理
线型可以看成一个由布尔值对应的像素。每种线型对应一定的长度的像素,每个像素对应相应的布尔值。如果该像素对应的布尔值为1,则绘制该像素。如果对应的布尔值为0,则不绘制该像素。
5. 区域填充法:扫描线法,边填充法,种子填充法,扫描线种子填充法,
扫描线法:
- 求交、排序、两两配对、线段着色,
- 注意顶点求交点规则:把所有极值顶点当成两个点
- (活性边表法好像不考?)边表的结构为 \([x,y_{max},\frac1k]\)。 $x: $当前扫描线与活性边的交点, $y_{max}: \(活性边较高端点的\)y$ 坐标值, $1k: $活性边所在直线斜率的倒数。

边填充法:该多边形每一条边右边区域像素的颜色全部取补
栅栏填充法:该多边形每一条边与栅栏之间像素的颜色全部取补
种子填充法:四连通/八联通,从某个像素点开始BFS/DFS整某个像素点开始个区域(缺点:堆栈大量使用)
扫描线种子填充法:
- 栈顶像素出栈。
- 沿扫描线对出栈像素的左右像素进行填充,直到遇到边界像素xl和xr为止
- 在区间[xl,xr]中检查与当前扫描线相邻的上下两条扫描线,则把每个 非边界、未填充 的 像素区间的最右像素取为种子像素入栈。
6. 反走样技术:像素细分技术,Bresenham反走样技术
像素细分技术
(1)将每个显示像素划分为若干个子像素。
(2)按照常规的计算方法计算出每个像素的颜色和亮度。
(3)采用算数平均或者加权平均等方法求解对应像素的亮度和颜色。
(4)显示出对应的像素。
Bresenham反走样技术:当待填充的多边形与具有一定面积的像素相交时,求出二者相交的面积,然后以此面积值来决定该像素应该显示的亮度和颜色。
Bresenham区域反走样算法首先将多边形每条边与具有一定面积的像素相交的面积大小分为8个等级,如果相交的面积小于1/8,则其灰度等级为0,介于1/8到2/8之间,则为1,依次类推。
\(S=(y_{i+1}+ y_i)/2=(y_i+ y_i+m)/2= y_i+m/2=e+m/2\),用e来确定像素的灰度值,注意将其映射到正的区间。
7. 曲线生成:Bezier曲线和B样条曲线,包括二阶、三阶曲线等。
二次Bezier曲线: 当控制点的个数为3时,可以得到Bezier曲线方程 \(P(t)=(1-t)^2P_0+2t(1-t)P_1+t^2P_2\quad t\in[0,1]\)
\[ \begin{aligned}&\text{用矩阵形式表示为}:\\&P(t)=[P_0,P_1,P_2]\begin{bmatrix}1&-2&1\\0&2&-2\\0&0&1\end{bmatrix}\begin{bmatrix}1\\t\\t^2\end{bmatrix}\quad t\in[0,1]\end{aligned} \]
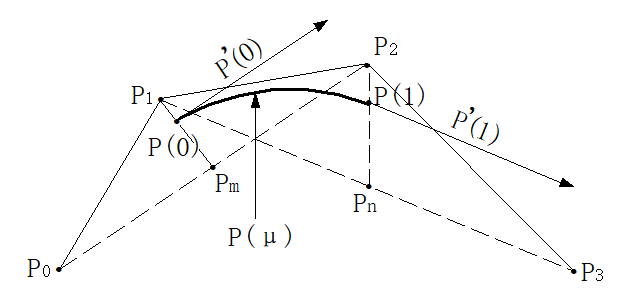
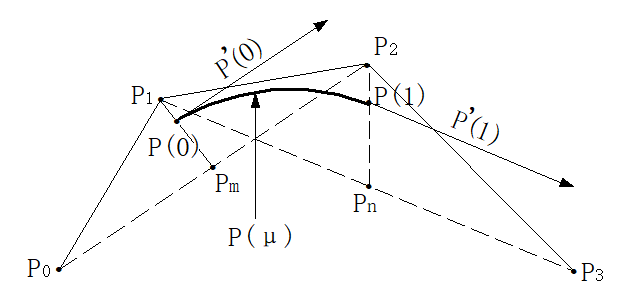
\[ \begin{aligned}\text{性质}:\\&\text{P}(0){=}P_0,\quad P(1){=}P_2,\quad\text{P}^{\prime}(0){=}2(\text{P}_1-\text{P}_0),\quad\text{P}^{\prime}(1){=}2(\text{P}_2-\text{P}_1)\\&\text{P}(0.5){=}\frac12(\text{P}_1+\frac12(P_0+\text{P}_2))=\frac12(\text{P}_1+\text{P}_m),\text{P}^{\prime}(0.5){=}\text{P}_2{-}\text{P}_0\end{aligned} \]

三次Bezier曲线: 当控制点的个数为4时,可以得到三次Bezier曲线方程: \(P(t)=(1-t)^3P_0+3t(1-t)^2P_1+3t^2(1-t)P_2+t^3P_3=B_{0,3}(t)P_0+B_{1,3}(t)P_1+B_{2,3}(t)P_2+B_{3,3}(t)P_3\quad t\in[0,1]\) \[ \begin{aligned}&\text{用矩阵形式表示为}:\\&P(t)=[P_0,P_1,P_2,P_3]\begin{bmatrix}1&-3&3&-1\\0&3&-6&3\\0&0&3&3\\0&0&0&1\end{bmatrix}\begin{bmatrix}1\\t\\t^2\\t^3\end{bmatrix}\quad t\in[0,1]\end{aligned} \]
\[ \begin{aligned}\text{性质:}\\&\mathsf P(0)=P_0,\quad P(1)=P_3,\quad\mathsf P'(0)=3(\mathsf P_1-\mathsf P_0),\quad\mathsf P'(1)=3(\mathsf P_3-\mathsf P_2)\\&\mathsf P''(0)=6(\mathsf P_0-\mathsf2\mathsf P_1+\mathsf P_2),\quad\mathsf P''(1)=6(\mathsf P_1-\mathsf2\mathsf P_2+\mathsf P_3)\end{aligned} \]
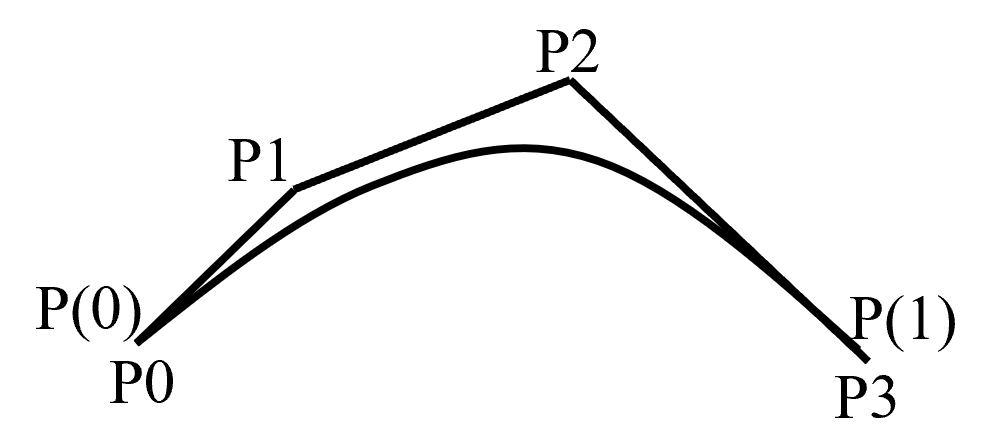
二次B样条曲线:在n=2控制点为3个时,可得到二次B样条曲线的定义为: \[ P(t)=\sum_{i=0}^2P_i\cdot B_{i,2}(t)=\frac12(t-1)^2P_0+\frac12(-2t^2+2t+1)P_1+\frac12t^2P_2 \]
\[ \begin{aligned} \text{性质:} \\ &\begin{aligned}\mathsf P(0)=\frac12(P_0+P_1)\quad\mathsf P(1)=\frac12(P_1+P_2)\quad\mathsf P'(0)=P_1-P_0\quad\mathsf P'(1)=P_2-P_1\end{aligned} \\ &\mathsf{P}(0.5)=\frac12(\frac12\left(\mathsf{P}(0)+\mathsf{P}(1)\right)+P_1)=\frac12(P_m+P_1)\quad P^{\prime}(0.5)=\mathsf{P}(1)-\mathsf{P}(0) \end{aligned} \]
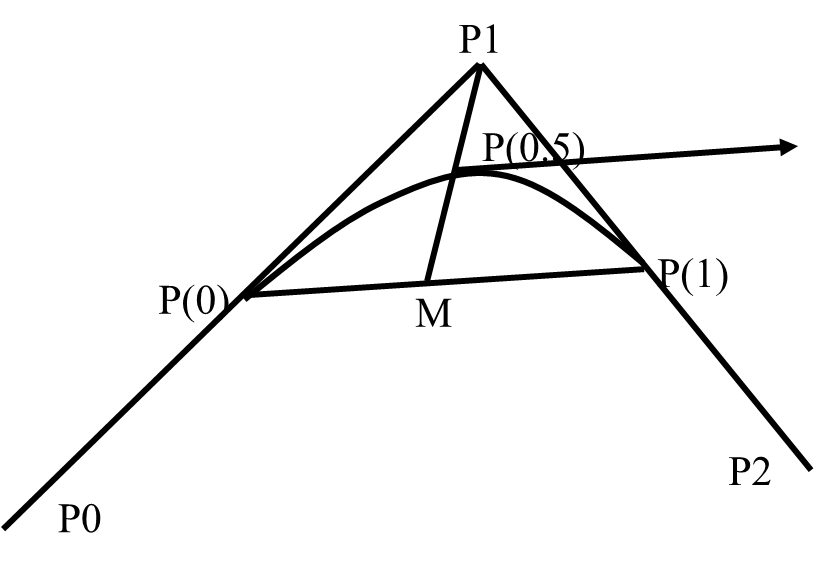
三次B样条曲线:在n=3控制点为4个时,可得到三次B样条曲线的定义为:
\[
P(t)=\sum_{i=0}^3P_i\cdot
B_{i,3}(t)=\frac16(-t^3+3t^2-3t+1)P_0+\frac16(3t^3-6t^2+4)P_1+\frac16\left(-3t^3+3t^2+3t+1\right)P_2+\frac16t^3P_3
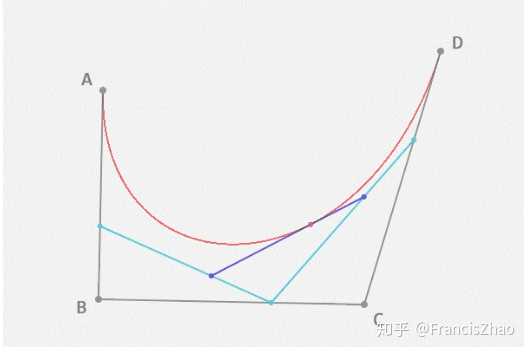
\] 三次B样条曲线的起点在三角形\(\Delta
P_0P_1P_2\)的中线\(P_1P_m\)上,且距离P1点的1/3处(不是中点!)。其切线方向与\(P_0P_2\)平行,且为底边长度的1/2。同样终点位于\(\Delta P_1P_2P_3\)的纵向\(P_2P_n\)上,且在距离P2点1/3处。其切线方向与\(P_1P_3\) ”平行,且为底边长度的1/2。 \[
\begin{aligned}\text{性质:}\\
&P_{0,3}(0)=\frac{1}{6}(P_{0}+4P_{1}+P_{2})=\frac{1}{3}(\frac{P_{0}+P_{2}}{2})+\frac{2}{3}P_{1}
\\
&P_{0,3}(1)=\frac{1}{6}\bigl(P_{1}+4P_{2}+P_{3}\bigr)=\frac{1}{3}\bigl(\frac{P_{1}+P_{3}}{2}\bigr)+\frac{2}{3}P_{2}
\\
&P_{0,3}^{\prime}(0)=\frac{1}{2}(P_{2}-P_{0}),P_{0,3}^{\prime}(1)=\frac{1}{2}(P_{3}-P_{1})
\end{aligned}
\]
8. 图形变化:平移、缩放、旋转
\[ T_{3D}=\begin{bmatrix}1&0&0&0\\0&1&0&0\\0&0&1&0\\b_x&b_y&b_z&1\end{bmatrix}S_{3D}=\begin{bmatrix}s_x&0&0&0\\0&s_y&0&0\\0&0&s_z&0\\0&0&0&1\end{bmatrix} \\\mathbf{R}_{\mathbf{x}}=\left[\begin{array}{cccc}1 & 0 & 0 & 0 \\0 & \cos \theta & \sin \theta & 0 \\0 & -\sin \theta & \cos \theta & 0 \\0 & 0 & 0 & 1\end{array}\right]\mathbf{R}_{\mathbf{y}}=\left[\begin{array}{cccc}\cos \theta & 0 & -\sin \theta & 0 \\0 & 1 & 0 & 0 \\\sin \theta & 0 & \cos \theta & 0 \\0 & 0 & 0 & 1\end{array}\right]\mathbf{R}_{\mathbf{z}}=\left[\begin{array}{cccc}\cos \theta & \sin \theta & 0 & 0 \\-\sin \theta & \cos \theta & 0 & 0 \\0 & 0 & 1 & 0 \\0 & 0 & 0 & 1\end{array}\right] \]
坐标行向量表达,变换矩阵×在右侧,逆时针为正方向
9. 坐标系之间的变换:局部坐标、世界坐标、摄像机坐标、屏幕坐标
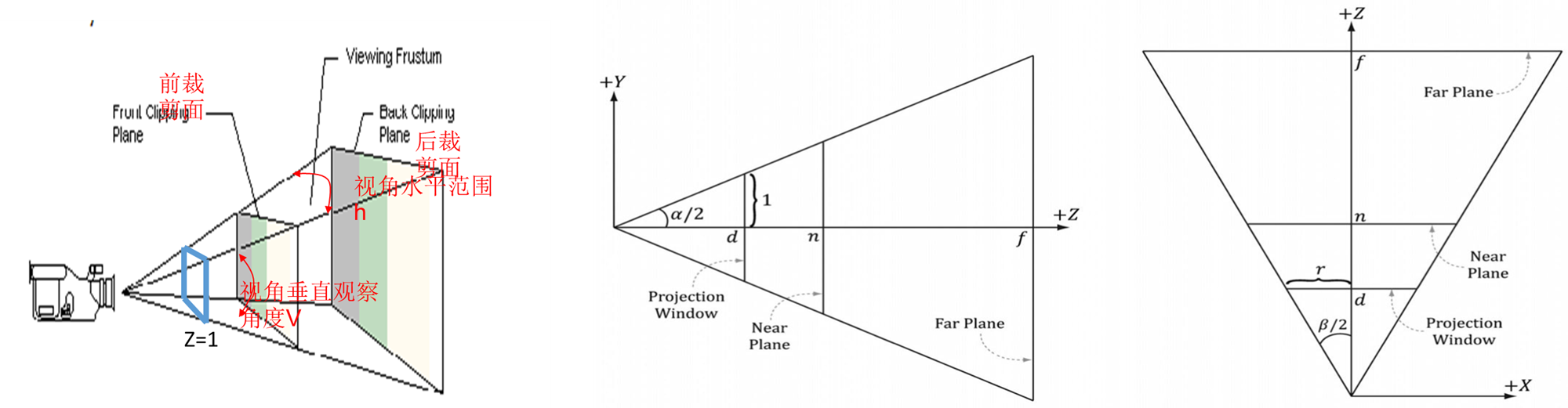
摄像机坐标(PPT) \[
\begin{align}
\left[x, y, z,
1\right]\begin{bmatrix}\dfrac{1}{r\tan\left(\alpha/2\right)}&0&0&0\\0&\dfrac{1}{\tan\left(\alpha/2\right)}&0&0\\
0&0&\dfrac{f}{f-n}&1\\
0&0&\dfrac{-nf}{f-n}&0\end{bmatrix}\quad&=\left[\dfrac{x}{r\tan\left(\alpha/2\right)},\dfrac{y}{\tan\left(\alpha/2\right)},\dfrac{zf-nf}{f-n},z\right]\\\text{规格化}&=
\left[\frac{x}{rz\tan\left(\alpha/2\right)},\frac{y}{z\tan\left(\alpha/2\right)},A+\frac{B}{z},1\right]
\end{align}
\] 
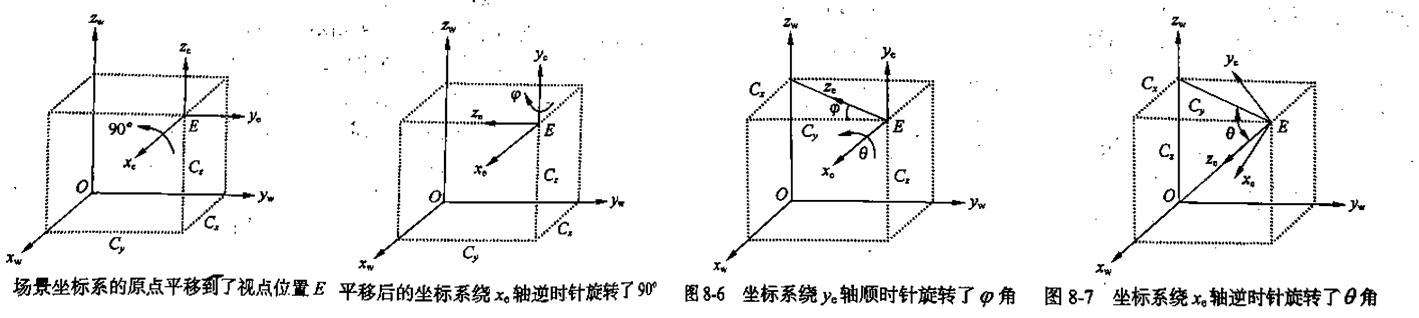
世界坐标 - 摄像机坐标
注意:坐标轴顺时针旋转,也就是场景逆时针选择。坐标轴变换对应的变换矩阵都是反向的。
- 步骤1:场景坐标系的原点从场景坐标系平移到视点位置 E(Cx,Cy,Cz)
- 步骤2:经过平移后的坐标系绕\(x_e\)轴逆时针旋转90°,
- 步骤3:坐标系绕\(y_e\)轴顺时针旋转角\(\varphi\),使新坐的z轴垂直指向原景物坐标系的Z轴,
- 步骤4:坐标系绕\(x_e\)轴顺时针旋转角\(\theta\),使新坐的z轴垂直指向原景物坐标系的原点,
- 步骤5:右手坐标系调整为左手坐标系,x轴反向
\[ \boldsymbol{T}_1=\begin{bmatrix}1&0&0&0\\0&1&0&0\\0&0&1&0\\-C_x&-C_y&-C_z&1\end{bmatrix} \boldsymbol{T}_2=\begin{bmatrix}1&0&0&0\\0&\cos(-90^\circ)&\sin(-90^\circ)&0\\0&-\sin(-90^\circ)&\cos(-90^\circ)&0\\0&0&0&1\end{bmatrix} \left.\boldsymbol{T}_{3}=\left[\begin{matrix}{\cos\varphi}&{0}&{-\sin\varphi}&{0}\\{0}&{1}&{0}&{0}\\{\sin\varphi}&{0}&{\cos\varphi}&{0}\\{0}&{0}&{0}&{1}\\\end{matrix}\right.\right] \boldsymbol{T}_{4}=\left[\begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & \cos \theta & -\sin \theta & 0 \\ 0 & \sin \theta & \cos \theta & 0 \\ 0 & 0 & 0 & 1 \end{array}\right] \boldsymbol{T}_5=\begin{bmatrix}-1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{bmatrix} \]
10. 四边形裁剪算法:Cohen-Sutherland裁剪算法、中点分割裁剪算法、Liang-Barskey裁剪算法
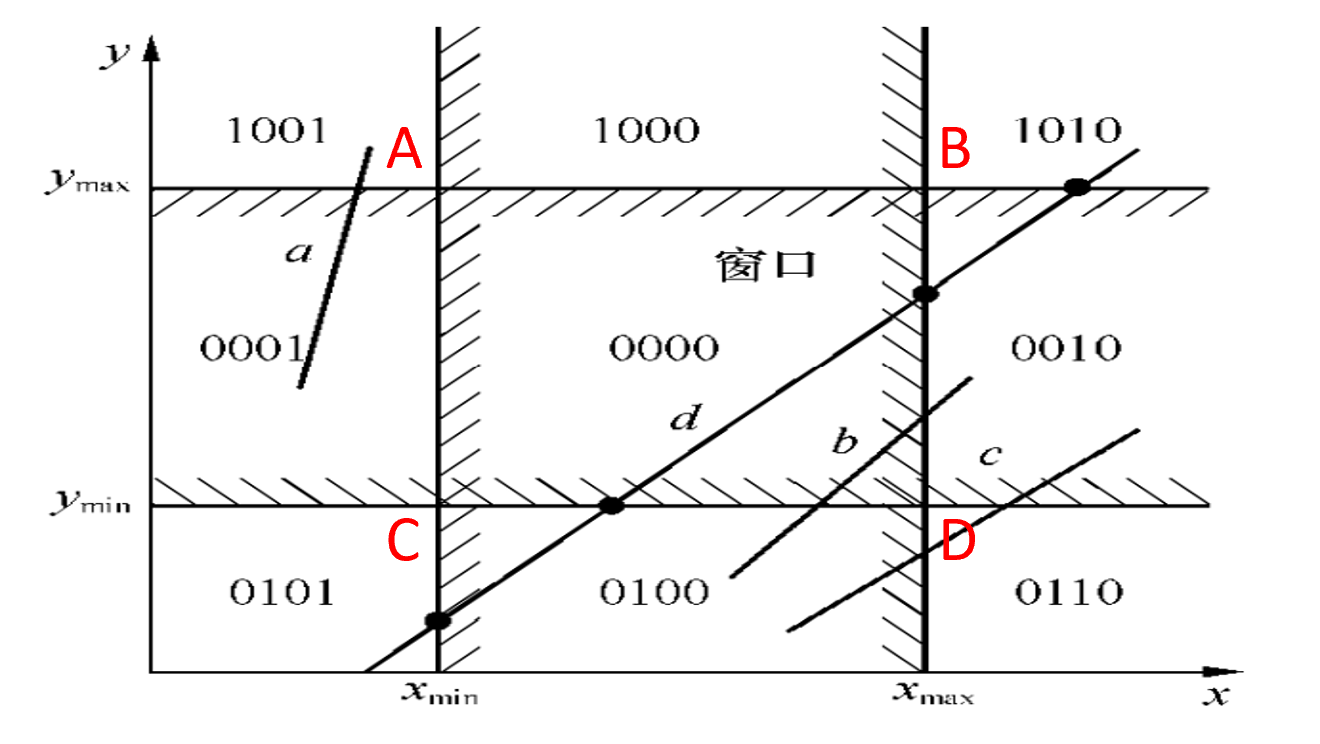
- Cohen-Sutherland裁剪算法(编码裁剪算法)
- 对线段端点编码,定义为它所在区域的编码;
- 快速判断“完全可见”,若两端点编码均为0,则完全可见。RC0=0且RC1=0
- 快速判断“完全不可见”,线段两端点编码的逻辑位“与”运算结果非零,则完全不可见。RC0&RC1≠0说明直线段位于窗外的同一侧
- 若2)、3)不满足,逐个端点判断其编码 CtCbCrCl(C3C2C1C0) 中位是否为“1”,若是,则需求交,交点的x坐标进行排序,从而将原始线段分割成最多五段线段(四个交点)。然后根据(1)(2)步判断这些线段是否在区域内。
中点分割裁剪算法
采用Cohen-Sutherland算法判断可见性
固定 P1,测试 P2是否在窗口内,若是,则 P2 是离 P1 点最远的可见点。否则,将线段 P1P2 对分,求出中点 Pm,编码判断线段 PmP2 是否全部在窗口外,若是,则舍弃PmP2,用 P1Pm代替 P1P2;若不是,则用PmP2代替P1P2。求得离P1最远的可见点Pm。
固定P2,再测 P1,
Liang(梁友栋)-Barsky裁剪算法
- 无论何种情况下,在裁剪区域之内的线段均为:AB ∩ RS ∩ TU

记\(L=\max \left[x_{\min }, \min \left(x_{A}, x_{B}\right)\right], R=\min \left[x_{\max }, \max \left(x_{A}, x_{B}\right)\right]\),不等式若有不成立,则不存在可见线段,不等式为: \[ \left\{\begin{array}{l} L \leqslant R \\ L \leqslant \max \left(x_{T}, x_{U}\right) \\ \min \left(x_{T}, x_{U}\right) \leqslant R \end{array}\right.; \quad \text{斜率>0时} \left\{\begin{array}{l} L \leqslant R \\ L \leqslant x_{U} \\ x_{T} \leqslant R \end{array}\right.; \quad \text{斜率<0时} \left\{\begin{array}{l} L \leqslant R \\ L \leqslant x_{T} \\ x_{U} \leqslant R \end{array}\right. \] A B 斜率大于 0 时,可见线段的端点坐标:\(\begin{array}{l} x_{\alpha}=\max \left(L, x_{T}\right) \\ x_{\beta}=\min \left(R, x_{U}\right) \end{array}\)
A B 斜率小于 0 时,可见线段的端点坐标:\(\begin{array}{l} x_{\alpha}=\max \left(L, x_{U}\right) \\ x_{\beta}=\min \left(R, x_{T}\right) \end{array}\)
11. 多边形裁剪算法:Sutherland-Hodgman算法,Weiler-Atherton算法
- Sutherland-Hodgman算法
- 裁剪凹多边形可能会出现多余的边
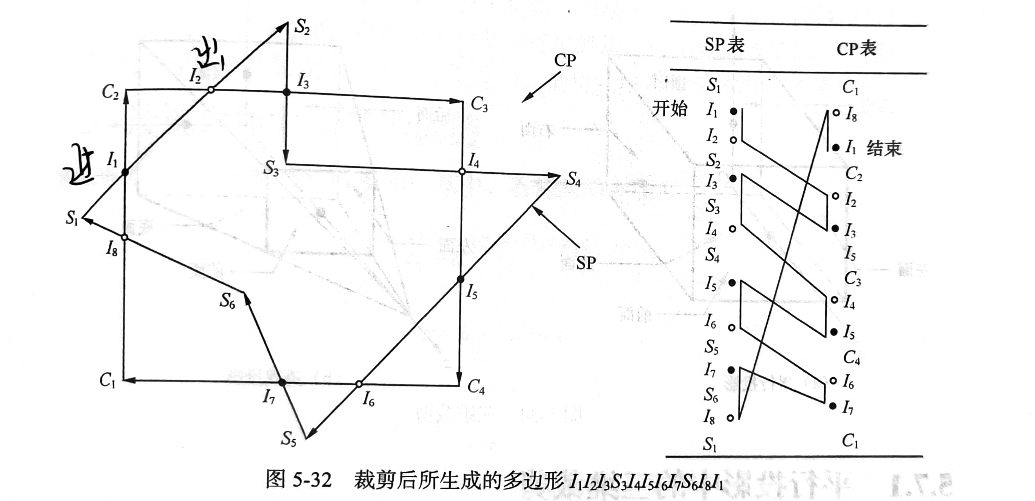
Weiler-Atherton算法
- 将裁剪多边形称为CP,被裁剪多边形称为SP。
- 算法首先将CP和SP的顶点按照外部边界取顺时针,内部边界取逆时针的的方式将其构成环形链表。
- 求SP与CP的所有交点,并将这些交点插入到SP和CP的环形链表中,并标明交点是出点还是进点(进入CP)。
- 算法从任意一个进点开始沿着SP的边线按照边线所标示的方向搜集顶点序列,当遇到出点时,则沿着CP的边线所标示的方向搜集顶点序列,当遇到进点时,则沿着SP的边线所标示的方向搜集顶点序列。
- 搜索所有点。
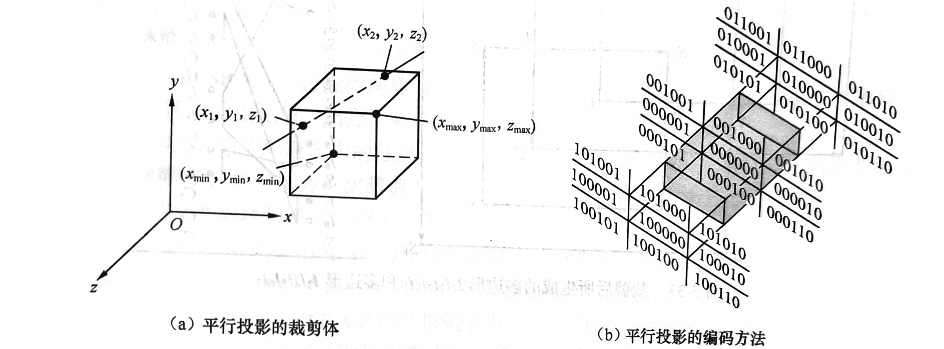
12. 三维线段裁剪算法:长方体裁剪算法,视椎体裁剪算法
长方体裁剪算法(编码裁剪算法)
- 采用6位二进制对不同区域进行编码,[前,后,上,下,右,左]
- 如果线段的两个端点的编码全部为0,则完全在长方体内部
- 同时位于长方体的一侧,则两端点编码对应位相与的结果必不为0,因此该线段完全不可见。
- 穿越立方体,则需要求交,然后将线段分割成几个部分,分别判断每一段线段是否可见。
视椎体裁剪
- 计算每个平面方程。如果对应的方程的值>0,表明在该平面之上……其他同长方体
13. 图形消隐:背面剔除算法,画家算法,Weiler-Atherton算法,BSP树算法、深度缓冲区算法,Warnock算法
- 背面剔除算法
计算多边形的法向向量N和视线向量V。
计算法向向量N和视线向量V的夹角θ的余弦Cosθ=N.V。
cosθ<0,即θ>90°, 则该多边形表面为背面,是不可见的
- 画家算法
- 将多边形按照离视点的远近进行排序(P221 判断遮挡,分割),然后先画出被遮挡的多边形,再画出不被遮挡的多边形,用后画的多边形覆盖先画的多边形,从而达到自动消隐的目的。
- Weiler-Atherton算法:采用裁剪算法的思想对隐藏面进行消隐。
- 先进行初步的深度预排序,即将变换到屏幕坐标系中的景物表面多边形按各顶点的 z 最小值进行排序,形成景物多边形表。
- 以当前具有最大 z 值(即离视点最近)的景物表面作为裁剪多边形 CP 。
- 用CP对景物多边形表中排在后面的景物表面进行裁剪,产生内部多边形 Pin 和外部多边形 Pout 。
- 由于多边形顶点离视点最近的多边形表面不一定是真正排在最前面的可见面,因此,需比较CP与内部多边形 Pin 的深度,检查 CP是否是真正离视点较近的多边形。 如果是,则CP为可见表面,而位于裁剪多边形 CP之内的多边形 Pin 为当前视点的隐藏面,可以消去该隐藏面;如果不是,则选择 Pin 为新的裁剪多边形,重复步骤 3。
- 将位于裁剪多边形之外的景物表面 Pout 组成外裁剪结果多边形表,取表中深度最大即排在最前面的表面为裁剪多边形,重复步骤 3,继续对表中其他景物表面进行裁剪。
- 上述过程递归进行,直到外裁剪结果多边形表为空时为止
- BSP树算法:平面分割二叉树
- 先在场景中选取一剖分平面 P1(与视点垂直的平面),将场景空间分割成两个半空间。它相应地把场景中的景物分成两组,相对于视点而言,一组景物多边形位于P1的前面,作为BSP树的左孩子(front),另一组景物多边形位于P1的后面,作为BSP树的右孩子(Back),如果有物体与 P1相交,就将它分割为两个物体分别标识为A和B,再用平面 P2 对所生成的两个子空间继续进行分割,并对每一子空间所含景物进行分类。上述空间剖分和景物分类过程递归进行,直至每一子空间中所含景物少于给定的阈值为止。
- 优先绘制标识为“back”的子空间中所含的景物,这样可使得前面的物体覆盖后面的物体,从而实现物体的消隐。
- 深度缓冲区算法:对投影到显示屏上的每一个像素所对应的多边形表面的深度进行比较,然后取最近表面的属性值作为该像素的属性值。深度缓冲器只是帧缓冲器的扩充。
- 将场景中的所有多边形通过取景变换、透视变换变换到屏幕坐标系中,物体的深度比较可通过它们z值的比较来实现。
- 初始化深度缓冲存储器和帧缓冲器。深度缓冲器应初始化为离视点最远的最大z值,帧缓冲器应初始化为背景的属性值。
- 扫描待显示的每一个多边形,比较当前多边形所覆盖的每一个像素点的深度值,如果其深度值比深度缓冲区中当前像素的深度值小,则取代原来的深度值,并将对应像素的属性值保存到帧缓冲区对应的位置中。反之,则不做任何处理。循环该步骤,直到处理完所有的多边形。
- Warnock算法:将非单纯的窗口四等分为4个子窗口(四叉树),对每个子窗口再进一步判别是否是单纯的,直到窗口单纯或窗口边长已缩减至一个像素点为止。
- 对每个窗口进行判断,若画面中所有多边形均与此窗口分离,即此窗口为空,则按背景光强或颜色直接显示而无需继续分割。
- 若窗口中仅包含一个多边形,则窗口内多边形外的区域按背景光强或颜色填充,多边形内按多边形相应的光强或颜色填充。
- 若窗口与一个多边形相交,则窗口内多边形外的区域按背景光强或颜色填充,相交多边形内位于窗口内的部分按多边形相应的光强或颜色填充。
- 若窗口被一个多边形包围且窗口内无其他的多边形,则窗口按此包围多边形相应的光强或颜色填充。
- 若窗口至少被一个多边形包围且此多边形距离视点最近,则窗口按此离视点最近的包围多边形的相应光强或颜色填充。
- 若以上条件都不满足,则继续细分窗口,并重复以上测试。
14. 曲面的生成:Bezier曲面的生成,B样条曲面的生成,特别是二阶和三阶曲面
二阶Bezier曲面 \[ P(u,v)=\sum_{i=0}^2\sum_{j=0}^2P_{ij}BEZ_{i,2}(u)BEZ_{j,2}(v)\quad u\in[0,1],v\in[0,1] \] 三阶Bezier曲面 \[ P(u,v)=\sum_{i=0}^3\sum_{j=0}^3P_{ij}BEZ_{i,3}(u)BEZ_{j,3}(v)\quad u\in[0,1],v\in[0,1]\\ =\begin{bmatrix}BEZ_{0,3}(u)&BEZ_{1,3}(u)&BEZ_{2,3}(u)&BEZ_{3,3}(u)\end{bmatrix}\begin{bmatrix}P_{00}&P_{01}&P_{02}&P_{03}\\P_{10}&P_{11}&P_{12}&P_{13}\\P_{20}&P_{21}&P_{22}&P_{23}\\P_{30}&P_{31}&P_{32}&P_{33}\end{bmatrix}\begin{bmatrix}BEZ_{0,3}(v)\\BEZ_{1,3}(v)\\BEZ_{2,3}(v)\\BEZ_{3,3}(v)\end{bmatrix}\\ =[(1-u)^3\quad3u(1-u)^2\quad3u^2(1-u)\quad u^3]\begin{bmatrix}P_{00}&P_{01}&P_{02}&P_{03}\\P_{10}&P_{11}&P_{12}&P_{13}\\P_{20}&P_{21}&P_{22}&P_{23}\\P_{30}&P_{31}&P_{32}&P_{33}\end{bmatrix}\begin{bmatrix}(1-\nu)^3\\3\nu(1-\nu)^2\\3\nu^2(1-\nu)\\\nu^3\end{bmatrix}\\ \begin{aligned}=[1\quad u\quad u^2\quad u^3]\boldsymbol{N}\begin{bmatrix}\boldsymbol{P}_{00}&\boldsymbol{P}_{01}&\boldsymbol{P}_{02}&\boldsymbol{P}_{03}\\\boldsymbol{P}_{10}&\boldsymbol{P}_{11}&\boldsymbol{P}_{12}&\boldsymbol{P}_{13}\\\boldsymbol{P}_{20}&\boldsymbol{P}_{21}&\boldsymbol{P}_{22}&\boldsymbol{P}_{23}\\\boldsymbol{P}_{30}&\boldsymbol{P}_{31}&\boldsymbol{P}_{32}&\boldsymbol{P}_{33}\end{bmatrix}\boldsymbol{N}^\intercal\begin{bmatrix}1\\v\\v^2\\v^3\end{bmatrix}\quad\text{其中:}\quad\boldsymbol{N}=\begin{bmatrix}1&-3&3&-1\\0&3&-6&3\\0&0&3&-3\\0&0&0&1\end{bmatrix},\end{aligned} \] 二阶B样条曲面 \[ P(u,\nu)=\sum_{i=0}^m\sum_{j=0}^nP_{ij}B_{i,k}(u)B_{j,h}(\nu)\quad u\in[0,1],\nu\in[0,1] \] 三阶B样条曲面 \[ \begin{aligned}P(u,\nu)&=\begin{bmatrix}B_{0,3}(u)&B_{1,3}(u)&B_{2,3}(u)&B_{3,3}(u)\end{bmatrix}\begin{bmatrix}P_{00}&P_{01}&P_{02}&P_{03}\\P_{10}&P_{11}&P_{12}&P_{13}\\P_{20}&P_{21}&P_{22}&P_{23}\\P_{30}&P_{31}&P_{32}&P_{31}\end{bmatrix}\begin{bmatrix}B_{0,3}(v)\\B_{1,3}(v)\\B_{2,3}(v)\\B_{3,3}(v)\end{bmatrix}\\ &=\begin{bmatrix}1&u&u^2&u^3\end{bmatrix}N\begin{bmatrix}P_{00}&P_{01}&P_{02}&P_{03}\\P_{10}&P_{11}&P_{12}&P_{13}\\P_{20}&P_{21}&P_{22}&P_{23}\\P_{30}&P_{11}&P_{32}&P_{33}\end{bmatrix}N^{\intercal}\begin{bmatrix}1\\v\\v\\v^2\\v^3\end{bmatrix},N=\frac16\begin{bmatrix}1&4&1&0\\-3&0&3&0\\3&-6&3&0\\-1&3&-3&1\end{bmatrix}\end{aligned} \]
\[ \begin{aligned} &B_{0,3}(u)=\frac16(-u^3+3u^2-3u+1), &B_{0,3}(\nu) &= \frac16(-\nu^3+3\nu^2-3\nu+1) \\ &B_{1,3}(u)=\frac16(3u^3-6u^2+4)\text{ ,} &B_{1,3}(\nu)&= \frac16(3\nu^3-6\nu^2+4) \\ &B_{2,3}(u)=\frac16(-3u^3+3u^2+3u+1), &B_{2,3}(\nu)&=\frac16(-3\nu^3+3\nu^2+3\nu+1) \\ &B_{3,3}(u)= \frac16\boldsymbol{u}^3, &B_{3,3}(\nu)&= \begin{aligned}\frac{1}{6}\nu^3\end{aligned} \end{aligned} \]
15. 地形的生成算法
- Diamond-Square算法
- 给定一个四边形,四个顶点的坐标(包含高度),定义一初始高度因子h和一缩放倍数b。
- 迭代,先求出四边形的中心点高度为顶点平均高度+h*r的随机数,再分别求出4个边的中点,高度为两端点高度的平均值+h*r
- 修正高度因子 h=h/b,用(2)的方法分别对这 4 个小正方形进行处理。直到达到所期望的山形细腻程度。
16. 雨雪的模拟算法
- 生成一定数量的初始粒子,对其各个属性进行赋值。
- 更新粒子的运动参数,比如速度,加速度,位置,生命周期等。
- 针对每一个粒子,在粒子对应的位置上绘制位图,并进行位移的映射,背景融合等。
- 删除已经消亡的粒子,释放其占用的资源。
\[ \begin{cases}\nu_x=\nu_x+\Delta t\cdot f/m\\\nu_y=\nu_y+\Delta t\cdot\left(g+f/m\right)\\\nu_z=\nu_z+\Delta t\cdot f/m&\end{cases}, \begin{cases}P_x=P_x+\nu_x\cdot\Delta t\\P_y=P_y+\nu_y\cdot\Delta t\\P_z=P_z+\nu_z\cdot\Delta t&\end{cases} \]
代码
DDA画直线

void Line_DDA(int x0, int y0, int x1, int y1, Color color)
{
// 计算delta_x, delta_y, 确定steps,并计算dx, dy
int delta_x = x1 - x0, delta_y = y1 - y0,
steps = max(abs(delta_x), abs(delta_y));
double x = x0, y = y0,
dx = (double)delta_x / steps, dy = (double)delta_y / steps;
for (int i = 1; i <= steps + 1; i++)
{
putpixel((int)(x + 0.5), (int)(y + 0.5), color); // 四舍五入生成像素点
x += dx, y += dy;
}
}中点画线法

void Line_Midpoint(int x0, int y0, int x1, int y1, Color color)
{
if (x0 > x1) // 保证x0 <= x1
swap(x0, x1), swap(y0, y1);
int a = y0 - y1, b = x1 - x0, // 直线L的参数(c因为没有用到不用计算)
d, // 决策变量d
dd_L, dd_G, // 决策变量d的增量(L代表小于0的情况,G代表大于0的情况)
x = x0, y = y0, // 初始P坐标
dPx_L, dPy_L, dPx_G, dPy_G; // P坐标的增量(L代表小于0的情况,G代表大于0的情况)
// 根据k值分情况生成决策变量和增量
if (-b <= a && a <= 0) // k ∈ [0, 1]
{
d = 2 * a + b; // d0 = 2a + b
dPx_L = 1, dPy_L = 1, dd_L = 2 * (a + b); // d < 0情况
dPx_G = 1, dPy_G = 0, dd_G = 2 * a; // d >= 0 情况
}
// 其他斜率情况略
// 迭代生成直线
while (x != x1 || y != y1)
{
putpixel(x, y, color);
if (d < 0)
x += dPx_L, y += dPy_L, d += dd_L;
else
x += dPx_G, y += dPy_G, d += dd_G;
}
putpixel(x, y, color);
}Bresenham 画线法

void Line_Bresenham(int x0, int y0, int x1, int y1, Color color)
{
if (x0 > x1) // 保证x0 <= x1
swap(x0, x1), swap(y0, y1);
int Delta_x = x1 - x0, Delta_y = y1 - y0,
d, // 决策变量d
dd_L, dd_G, // 决策变量d的增量(L代表小于0的情况,G代表大于0的情况)
x = x0, y = y0, // 初始P坐标
dPx_L, dPy_L, dPx_G, dPy_G; // P坐标的增量(L代表小于0的情况,G代表大于0的情况)
// 根据k值分情况生成决策变量和增量
if (0 <= Delta_y && Delta_y <= Delta_x) // k ∈ [0, 1]
{
d = 2 * Delta_y - Delta_x; // d0 = 2Δy - Δx
dPx_L = 1, dPy_L = 0, dd_L = 2 * Delta_y; // d < 0情况
dPx_G = 1, dPy_G = 1, dd_G = 2 * (Delta_y - Delta_x); // d >= 0 情况
}
// 其他斜率情况略
// 迭代生成直线
while (x != x1 || y != y1)
{
putpixel(x, y, color);
if (d < 0)
x += dPx_L, y += dPy_L, d += dd_L;
else
x += dPx_G, y += dPy_G, d += dd_G;
}
putpixel(x, y, color);
}中点画圆法

void DrawCirclePoints(int xc, int yc, int x, int y, Color color)
{
putpixel(xc + x, yc + y, color);
putpixel(xc + y, yc + x, color);
putpixel(xc - x, yc + y, color);
putpixel(xc + y, yc - x, color);
putpixel(xc + x, yc - y, color);
putpixel(xc - y, yc + x, color);
putpixel(xc - x, yc - y, color);
putpixel(xc - y, yc - x, color);
}
void Circle_Midpoint(int xc, int yc, int R, Color color)
{
int x = 0, y = R, // 初始P坐标
d = 1 - R; // 决策变量d
while (x < y)
{
DrawCirclePoints(xc, yc, x, y, color);
if (d < 0)
d += 2 * x + 3, x++;
else
d += 2 * (x - y) + 5, x++, y--;
}
DrawCirclePoints(xc, yc, x, y, color);
}Bresenham 画圆法

// DrawCirclePoints()函数已在中点画圆法给出,这里不再给出
void Circle_Bresenham(int xc, int yc, int R, COLORREF color)
{
int x = 0, y = R, // 初始P坐标
d = 2 - 2 * R; // 决策变量d
while (x < y)
{
DrawCirclePoints(xc, yc, x, y, color);
if (d < 0 && 2 * (d + y) - 1 <= 0)
d += 2 * x + 3, x++;
else
d += 2 * (x - y + 3), x++, y--;
}
DrawCirclePoints(xc, yc, x, y, color);
}