【编程训练】登山问题 - 梯度上升法
注意!此题目版权归本人指导老师卢鹏所有,禁止外传!
问题描述
有一座小山,其表面方程可以用 \(z=1-x^2-2y^2\) 底部为 \(xOy\) ,记起点为 \(P(0.7,0.5,0.01)\) ,从该起点开始爬山,要求登山线路沿着梯度方向前进。试着研究一下从起点到顶点的登山曲线。
计算注意要点:
- 每个具体位置的梯度方向并不完全相同,所以必须采用逐步迭代的方法登上山顶;
- 因为梯度有两个方向(x和y),所以不能简单取一个步长,合理的方式可以在梯度方向 上取单位向量并乘以取定步长(参考值 0.01)来确定x和y方向上的变化;
- 判断登上山顶条件,可以取高度大于 0.9999 即为登顶。(循环退出条件);
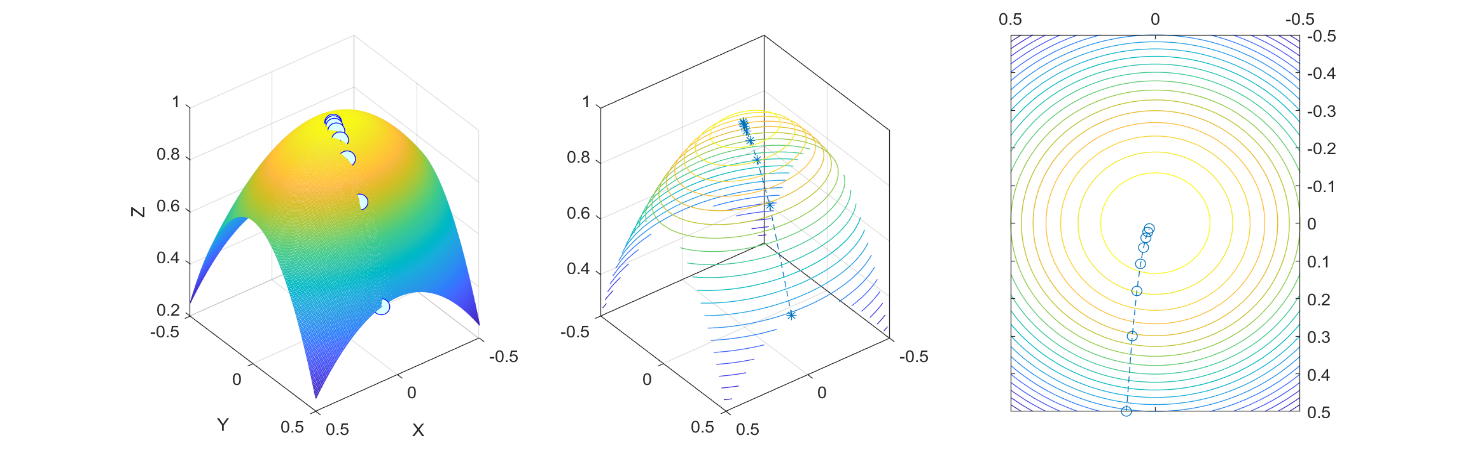
- 函数的空间图形与空间登上曲线画在一个图形里面;
- 平面线路图形的意思是需要画出空间曲线在平面中的投影曲线以及函数的等高线。 注:方法并不唯一,同学们也可以发挥想象完成此题!
结果展示
梯度上升法代码
对于相同的题型,仅需要修改下面三个function。
此外可以调整主函数的迭代参数。
[MATLAB] f.m 原函数
function z = f(x,y)
z=1-x.*x-2*y.*y;
end[MATLAB] fx.m 偏导x
function k = fx(x,y)
k=-2*x;
end[MATLAB] fy.m 偏导y
function k = fy(x,y)
k=-4*y;
end[MATLAB] main.m 主程序
%%开始绘图
clear;clc;
x=[-0.5:0.005:0.5];
y=[-0.5:0.005:0.5];
[X,Y]=meshgrid(x,y);
%Z=1-X.*X - 2*Y.*Y;
Z=f(X,Y);
%%迭代和绘图
figure(1);
hold on;
subplot(1,3,1);
mesh(X,Y,Z);%绘制三维图
xlabel('X');ylabel('Y');zlabel('Z');
hold on;
x0=0.1;y0=0.5; %起始点
z0=f(x0,y0);
way_x=[x0];way_y=[y0];way_z=[z0];
t=0.1; %步长:方向向量*t
%%开始迭代 梯度上升
while z0<0.999 && t>0.00001
x1=x0+fx(x0,y0)*t;% fx为偏x
y1=y0+fy(x0,y0)*t; %fy为偏y
z1=f(x1,y1);
if(z1>z0) %防止步长过大
x0=x1;
y0=y1;
z0=z1;
way_x(end+1)=x0; %记录迭代路径
way_y(end+1)=y0;
way_z(end+1)=z0;
else
t=t*0.1; %步长过大,“降温”
end
end
%%开始绘图
plot3(way_x,way_y,way_z,'-o','Color','b','MarkerSize',10,...,
'MarkerFaceColor','#D9FFFF');% 绘制迭代点
camorbit(180,0,'data',[0 0 1])% 转180度方便看
subplot(1,3,2); %三维等高线和迭代图
contour3(X,Y,Z,20);
hold on;
plot3(way_x,way_y,way_z,'*--')
camorbit(180,0,'data',[0 0 1]) % 转180度方便看
subplot(1,3,3); %平面等高线和迭代图
contour(X,Y,Z,20);
hold on;
plot3(way_x,way_y,way_z,'o--')
camorbit(180,0,'data',[0 0 1]) % 转180度方便看
hold off;补充
梯度下降法是一种“显而易见”的方法,其思维复合常理没有太多难度所以在这里不对该方法进行详细叙述。
基于梯度下降法和其思想诞生了很多行之有效的方法,例如动量梯度下降法、自适应梯度算法等改进算法,这种改进思想可以在很多算法上得到运用。