【编程训练】旅行商问题(TSP) - 遗传算法
注意!此题目版权归本人指导老师卢鹏所有,禁止外传!
问题描述
某公司计划在某个地区做广告选宣传,推销员从城市 1 出发,经过各个乡镇,再回到城市 1,城镇的坐标位置见下表。为节约开支,公司希望推销员走过这 50 个城镇的总距离最少,请你使用 LINGO 和 MATLAB 软件编程求出最少总距离及其路径(需画出最后的线路图)。
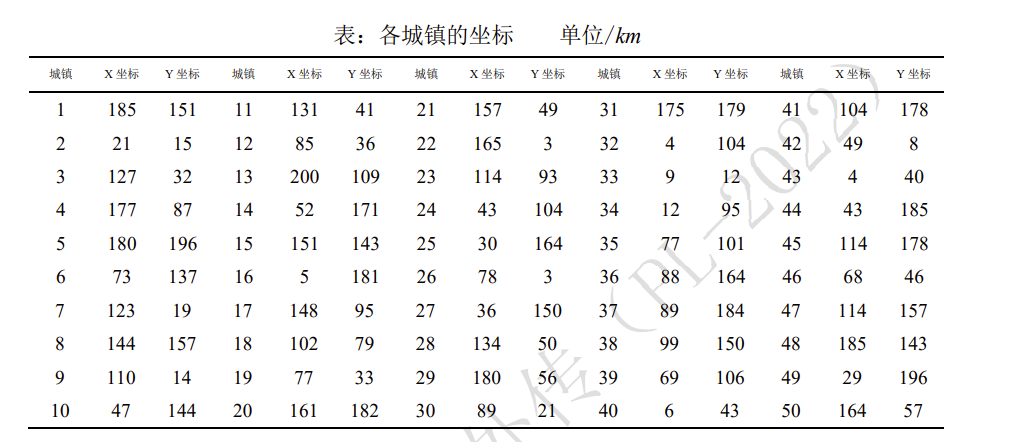
数学模型:
\[\min \sum_{i \neq j} d_{i j} x_{i j}\] \[s.t. \left\{ \begin{array}{l} \sum\nolimits_{j=1}^{50} x_{i j}=1, i=1,2, \ldots, 50 , ,\small (每个点只有一条边出去),\\ \sum\nolimits_{i=1}^{50} x_{i j}=1, j=1,2, \ldots, 50, \small (\text { 每个点只有一条边进去), } \\ \sum\nolimits_{i, j \in s} x_{i j} \leq|s|-1,2 \leq|s| \leq n-1, s \subset\{1,2, \ldots, 50\},\\ \small 即 S 为 \{1,2, \ldots, 50\} 的真子集 (除终点和起点外, 各边不构成圈), \\ x_{i j} \in\{0,1\}, i, j=1,2, \ldots 50, i \neq j \end{array}\right. \]
说明:
采用 LINGO 求解主要是约束当中第三个不好写,可以采用下面的约束替换:
计算详细步骤略。
\[{} \text { \small 破圈约束: } \quad u_{i}-u_{j}+n x_{i j} \leq n-1 ; u_{i}, u_{j} \geq 0 ; i=1,2, \cdots, n ; j=2, \cdots, n ; i \neq j\]
遗传算法代码
LINGO
model:
set:
c/1..50/:xco,yco,u;
link(c,c):d,x; !d表示距离,x表示路径;
endsets
data:
xco=185 21 127 177 180 73 123 144 110 47
131 85 200 52 151 5 148 102 77 161
157 165 114 43 30 78 36 134 180 89
175 4 9 12 77 88 89 99 69 6
104 49 4 43 114 68 114 185 29 164;
yco=151 15 32 87 196 137 19 157 14 144
41 36 109 171 143 181 95 79 33 182
49 3 93 104 164 3 150 50 56 21
179 104 12 95 101 164 184 150 106 43
179 8 40 185 178 46 157 143 196 57;
enddata
@for(link(i,j): !初始化d;
d(i,j)=@if(i #ne#j ,
@sqrt( (xco(i)-xco(j))*(xco(i)-xco(j)) + (yco(i)-yco(j))*(yco(i)-yco(j))),
100000);
);
min = @sum(c(i):@sum(c(j):d(i,j)*x(i,j)));
!破圈约束;
n = @size(c);
@for(link(i,j)|i #ne# j #and# i #ne# 1 #and# j #ne# 1:
u(i) - u(j) + n * x(i,j) <= n - 1
);
@for(c(i):
@sum(c(j)|i #ne# j :x(i,j))=1; !约束出度为1;
@sum(c(j)|i #ne# j :x(j,i))=1; !约束入度为1;
);
@for(link(i,j):@bin(x(i,j))); !约束x为0-1,可以不要;
end未优化MATLAB
%%数据初始化
clc;clear;
xco=[185 21 127 177 180 73 123 144 110 47 131 85 200 52 151 5 148 102 77 161 157 165 114 43 30 78 36 134 180 89 175 4 9 12 77 88 89 99 69 6 104 49 4 43 114 68 114 185 29 164];
yco=[151 15 32 87 196 137 19 157 14 144 41 36 109 171 143 181 95 79 33 182 49 3 93 104 164 3 150 50 56 21 179 104 12 95 101 164 184 150 106 43 79 8 40 185 178 46 157 143 196 57];
city_n=size(xco,2);
for i = 1:1:city_n
for j = 1:1:city_n
dis(i,j)=sqrt((xco(i)-xco(j))*(xco(i)-xco(j))+(yco(i)-yco(j))*(yco(i)-yco(j)));
end
end
%%遗传算法
%生成初始路径
best_way=[];best_fit=0;best_dist=0;new=0;
fit_time=[];dis_time=[];
way_n=10;
for i = 1:way_n
way0(i,:)=randperm(city_n);
end
%开始迭代
for o = 1:100000
way=way0;
for i = 1:way_n
d(i)=fit(way(i,:),dis);%路径距离
end
v=ones([1,way_n])*sum(d)./d;%适应度
for i = 1:way_n
if v(i)>best_fit
best_fit=v(i);
best_way=way(i,:);
best_dist=d(i);
new=1;
end;
end
v=v/sum(v);%选择概率
q=v(1);
for i = 2:way_n
q(i)=q(i-1)+v(i);%累积概率
end
for l = 1:5
%选择第一条路
q_rand = rand();
k=1;%为选择的路径编号
for i = 1:way_n
if q_rand>q(i)
k=i+1;
end
end
way1=k;
%选择第二条路
q_rand = rand();
k=1;%为选择的路径编号
for i = 1:way_n
if q_rand>q(i)
k=i+1;
end
end
way2=k;
%交配
q_rand = rand();
if(q_rand<0.9 && i~=j)
ran1 = randi([1,city_n]);
ran2 = randi([1,city_n]);
%交叉互换
for i = ran1:ran2
k=way(way1,i);
way(way1,i)=way(way2,i);
way(way2,i)=k;
end
%查重与去重way1
mark=zeros([1,city_n]);
for i = 1:city_n
mark(way(way1,i))=mark(way(way1,i))+1;
end
p1=[];p2=[];
for i = 1:city_n
if mark(i)==0
p1(end+1)=i;
end
if mark(i)==2
p2(end+1)=i;
end
end
ran=randperm(size(p1,2));%随机化
for i = 1:size(p2,2);
for j = 1:city_n
if (j<ran1 || j>ran2) && way(way1,j)==p2(i)
way(way1,j)=p1(ran(i));
break;
end
end
end
%查重与去重way2
mark=zeros([1,city_n]);
for i = 1:city_n
mark(way(way2,i))=mark(way(way2,i))+1;
end
p1=[];p2=[];
for i = 1:city_n
if mark(i)==0
p1(end+1)=i;
end
if mark(i)==2
p2(end+1)=i;
end
end
ran=randperm(size(p1,2));%随机化
for i = 1:size(p2,2);
for j = 1:city_n
if (j<ran1 || j>ran2) && way(way2,j)==p2(i)
way(way2,j)=p1(ran(i));
break;
end
end
end
%
end
%变异
q_rand = rand();
if(q_rand<0.2)
ran1 = randi([1,city_n]);
ran2 = randi([1,city_n]);
k=way(way1,ran1);
way(way1,ran1)=way(way1,ran2);
way(way1,ran2)=k;
ran1 = randi([1,city_n]);
ran2 = randi([1,city_n]);
k=way(way2,ran1);
way(way2,ran1)=way(way2,ran2);
way(way2,ran2)=k;
end
%存储为下一代
way0(l*2-1,:)=way(way1,:);
way0(l*2,:)=way(way2,:);
end
%绘图
figure(1)
if new==1
new=0;
gox=[];goy=[];
for i= 1:city_n
gox(i)=xco(best_way(i));
goy(i)=yco(best_way(i));
end
gox(end+1)=xco(best_way(1));
goy(end+1)=yco(best_way(1));
plot(gox,goy,'o--');
title(best_fit,best_dist);
drawnow;
%pause(0);
end
fit_time(end+1)=best_fit;
dis_time(end+1)=best_dist;
end
figure(2)
plot(fit_time);
figure(3)
plot(dis_time);
clear ran d i j k l o mark new p1 p2 l q q_rand ran1 ran2 v way way0 way1 way2 ;
clear dis gox goy xco yco;优化后MATLAB
%%数据初始化
clc;clear;
xco=[185 21 127 177 180 73 123 144 110 47 131 85 200 52 151 5 148 102 77 161 157 165 114 43 30 78 36 134 180 89 175 4 9 12 77 88 89 99 69 6 104 49 4 43 114 68 114 185 29 164];
yco=[151 15 32 87 196 137 19 157 14 144 41 36 109 171 143 181 95 79 33 182 49 3 93 104 164 3 150 50 56 21 179 104 12 95 101 164 184 150 106 43 79 8 40 185 178 46 157 143 196 57];
city_n=size(xco,2);
for i = 1:1:city_n
for j = 1:1:city_n
dis(i,j)=sqrt((xco(i)-xco(j))*(xco(i)-xco(j))+(yco(i)-yco(j))*(yco(i)-yco(j)));
end
end
%%遗传算法
%生成初始路径
best_way=[];best_fit=0;best_dist=100000;new=0;%记录最优解
fit_time=[];dis_time=[];%记录最优解变化
way_n=10;
for i = 1:way_n
way0(i,:)=randperm(city_n);
end
%开始迭代
for o = 1:10000
way=way0;
for i = 1:way_n
d(i)=fit(way(i,:),dis);%路径距离
end
v=ones([1,way_n])*sum(d)./d;%适应度
for i = 1:way_n
if d(i)<best_dist %改动1:以距离评判最优解
best_fit=v(i);
best_way=way(i,:);
best_dist=d(i);
new=1;
end;
end
v=v/sum(v);%选择概率
q=v(1);
for i = 2:way_n
q(i)=q(i-1)+v(i);%累积概率
end
for l = 1:5
%选择第一条路
q_rand = rand();
k=1;%为选择的路径编号
for i = 1:way_n
if q_rand>q(i)
k=i+1;
end
end
way1=k;
%选择第二条路
q_rand = rand();
k=1;%为选择的路径编号
for i = 1:way_n
if q_rand>q(i)
k=i+1;
end
end
way2=k;
%交配
q_rand = rand();
if(q_rand<0.9 && i~=j)
ran1 = randi([1,city_n]);
ran2 = randi([1,city_n]);
%交叉互换
for i = ran1:ran2
k=way(way1,i);
way(way1,i)=way(way2,i);
way(way2,i)=k;
end
%查重与去重way1
mark=zeros([1,city_n]);
for i = 1:city_n
mark(way(way1,i))=mark(way(way1,i))+1;
end
p1=[];p2=[];
for i = 1:city_n
if mark(i)==0
p1(end+1)=i;
end
if mark(i)==2
p2(end+1)=i;
end
end
ran=randperm(size(p1,2));%随机化
for i = 1:size(p2,2);
for j = 1:city_n
if (j<ran1 || j>ran2) && way(way1,j)==p2(i)
way(way1,j)=p1(ran(i));
break;
end
end
end
%查重与去重way2
mark=zeros([1,city_n]);
for i = 1:city_n
mark(way(way2,i))=mark(way(way2,i))+1;
end
p1=[];p2=[];
for i = 1:city_n
if mark(i)==0
p1(end+1)=i;
end
if mark(i)==2
p2(end+1)=i;
end
end
ran=randperm(size(p1,2));%随机化
for i = 1:size(p2,2);
for j = 1:city_n
if (j<ran1 || j>ran2) && way(way2,j)==p2(i)
way(way2,j)=p1(ran(i));
break;
end
end
end
%
end
%变异1:交换两点
q_rand = rand();
if(q_rand<0.2)
ran1 = randi([1,city_n]);
ran2 = randi([1,city_n]);
k=way(way1,ran1);
way(way1,ran1)=way(way1,ran2);
way(way1,ran2)=k;
ran1 = randi([1,city_n]);
ran2 = randi([1,city_n]);
k=way(way2,ran1);
way(way2,ran1)=way(way2,ran2);
way(way2,ran2)=k;
end
%改动2
%变异2:路径翻折 能有效防止路径交叉、加速迭代出最优解的改动
q_rand = rand();
if(q_rand<0.2) %概率越大,迭代优解速度越快,但解微微变差
ran1 = randi([1,city_n]);
way3=[];
for i = 1:city_n %存储旋转
way3(mod(i+ran1,city_n)+1)=way(way1,i);
end
ran1 = randi([1,city_n]);
ran2 = randi([1,city_n]);
if(ran1>ran2)
k=ran1;
ran1=ran2;
ran2=k;
end
for i = ran1 : (ran2+ran1)/2;%翻转
k=way3(i);
way3(i)=way3(ran2+ran1-i);
way3(ran2+ran1-i)=k;
end
way(way1,:)=way3;
end
%存储为下一代
way0(l*2-1,:)=way(way1,:);
way0(l*2,:)=way(way2,:);
ran = randi([1,way_n]);
way0(ran,:)=best_way; %改动3 :最显著的改动
end
%绘图
figure(1)
if new==1
new=0;
gox=[];goy=[];
for i= 1:city_n
gox(i)=xco(best_way(i));
goy(i)=yco(best_way(i));
end
gox(end+1)=xco(best_way(1));
goy(end+1)=yco(best_way(1));
plot(gox,goy,'o--');
title(best_fit,best_dist);
drawnow;
%pause(0);
end
fit_time(end+1)=best_fit;
dis_time(end+1)=best_dist;
end
figure(2)
plot(fit_time);
figure(3)
plot(dis_time);
clear ran d i j k l o mark new p1 p2 l q q_rand ran1 ran2 v way way0 way1 way2 ;
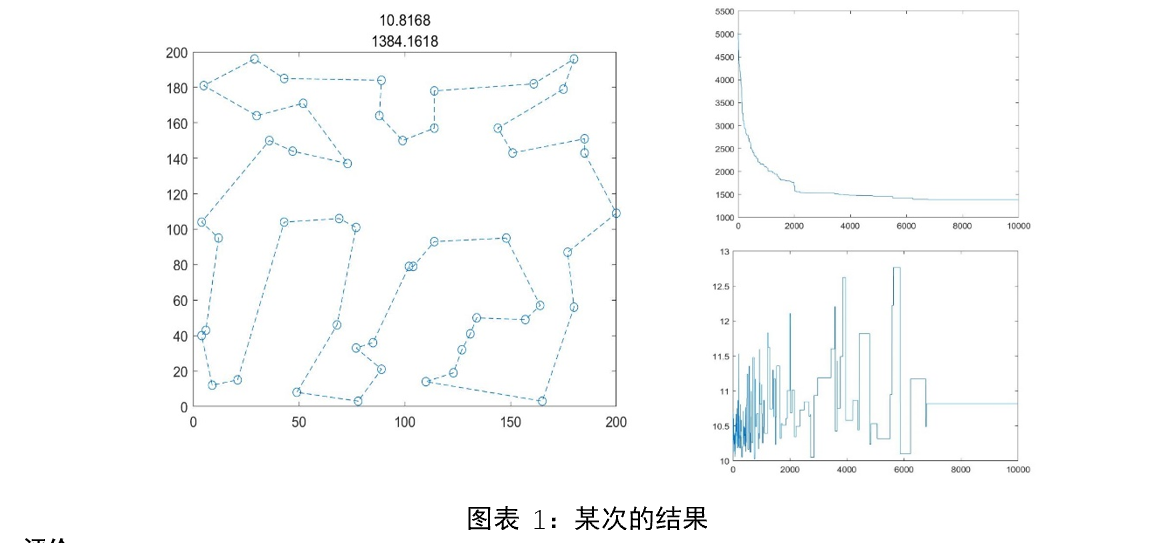
clear dis gox goy xco yco;结果说明
评价:
- 经过多次迭代检验,新的程序能在减少一个数量级的迭代次数情况下,每次都能得到一个近似的最优解(局部最优解),且其效率快,得到结果较优。
- 同时注意到其适应度迭代曲线,反应适应度(竞争优势度)并不能很好反应个体的优劣,猜想得验证。
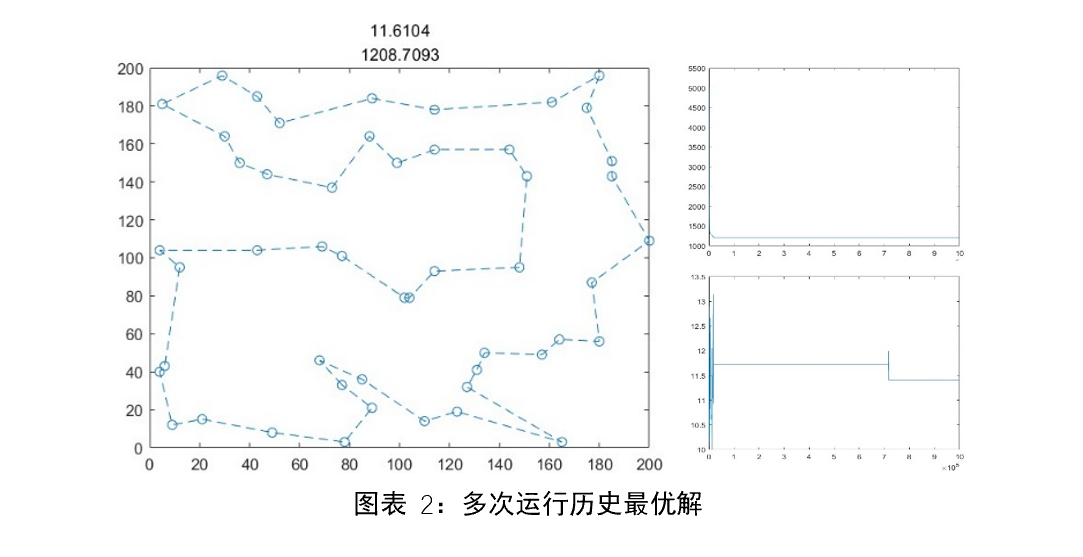
依然存在的问题:
经过手动多次迭代才找到了一个几乎是最优的解。根据迭代曲线可以看出解在前段已经收敛,且极难跳出当前解,而解的产生很大程度上取决于随机的初始化以及随机过程。为让解进一步迭代和增大单次运行找到最优解的可能性,应该引入更多可能的变异情况,而走出因为变异的单一性和局限性导致难以产生更优解的情况。
Ps:虽然我有想法,但是懒得改了。