聚类分析

聚类分析（Cluster Analysis）
又称为群分析，是对多个样本(或指标)进行定量分类的一种多元统计分析。对样本进行分析称为Q型聚类分析，对指标进行分类称为R型聚类分析^[1]。聚类与分类的不同在于，聚类所要求划分的类是未知的。

聚类是将数据分类到不同的类或者簇这样的一个过程，所以同一个簇中的对象有很大的相似性，而不同簇间的对象有很大的相异性^[2]。组内相似性越大，组间差距越大，说明聚类效果越好。

聚类效果的好坏依赖于两个因素：1.衡量距离的方法（distance measurement） 2.聚类算法（algorithm）^[3]

相似性衡量

相似性衡量（similarity measurement）
可近似为距离的计算（distance measurement）
距离，是抽象化的相似程度度量，不同的数据类型有着不同的距离计算方法，我们需要用数量化的方法刻画事物之间的相似程度。

1. 样本间距离度量

对于 $m$ 个指标描述的样本可以看成是 $\text{bold}{R}^m$ 空间中的一个点，自然用距离衡量样本的相似度。

1.1 数值变量

在做距离计算前，还需要对数据做标准化处理 $x_i^{\ast }=\frac{x_i-mea{n}_x}{S_x}$ ，以防止量纲的不同导致空间拉伸距离失真。

闵氏(Minkowski)距离： $$

以下均为闵氏(Minkowski)距离的子式

• 曼哈顿(Manhattan)距离：$$ 时 $$

• 欧几里得(Euclid)距离：$$ 时 （坐标轴正交旋后转保持不变） $$

• 切比雪夫(Chebyshev)距离：$$ 时 $$

对于不同的指标有不同的权重，还可以对上述公式的距离加权。将上述式子中 $$ 替换为 $$ (第一个和第三个式子会使加权与结果非线性)。此外使用闵氏(Minkowski)距离时，变量的多重相关性(Multicollinearity)会导致信息重叠，片面强调某些变量的重要性。因为上述缺点，一种改进的距离是马氏距离^[1]。

• 马氏(Mahalanobis)距离： $$ 其中：$$ 来自总体 $$ 的样本观测值；$$ 为 $$ 的协方差矩阵。

马氏距离对一切线性变换是不变的，故而不受量纲影响。

根据聚类分析目的或者指标的不同，还可以使用夹角余弦等方法度量相似度（数据挖掘拓展）。

1.2 二元变量

构造二元变量为0-1虚拟变量 |Name|指标1|指标2|指标3|指标4|指标5|指标6| |:-:|:-:|:-:|:-:|:-:|:-:|:-:| |Eirc|1|0|1|1|0|0| |Freddie|1|0|0|1|1|1| |Dramwig|0|1|1|1|1|0|

构造列联表

X	1	0	sum
1	a	b	a+b
0	c	d	c+d
sum	a+c	b+d	a+b+c+d

构造 $$

1.3 分类变量

• 简单匹配：$$ p为类别数，m为配对数
• 二元化：$$ $$ $$ ; $$ ; $$,

1.4 有序变量

1. 记序列为$$
2. z-scores来标准化 $$ 得 $$
3. 计算马氏(Minkowski)距离

2. 类与类间距度量

记两个类分别为 $$、$$，有以下方法度量类间距。

• 最短距离法（Nearest Neighbor or Single Linkage Method）： $$

• 最长距离法（Farthest Neighbor or Complete Linkage Method）： $$

• 重心法（Centetoid Method） $$

• 类平均法（Group Average Method）(被认为是最常用也最好用的方法其单调性良好，空间扩张/浓缩的程度适中) $$

• 离差平方和法（Sum of Squares Method）又称 Ward 方法

记 $$

$$

定义 $$

含义：$$、$$ 内点很聚集 $$、$$ 就会很小，即自聚为一类；$$、$$ 相聚很远则 $$ 很大，即 $$、$$ 充分分离。

3. 指标间距离度量

• 相关系数

$$

• 夹角余弦

$$

聚类算法

聚类算法多种多样，搭配上不同的相似性衡量算法对于聚类结果有巨大的差异。一下只给出了几种最根本的聚类算法，其他算法大都是在此基础上的优化与改进。这个回答可以窥视向外的拓展。

K-均值聚类(k-means)

步骤

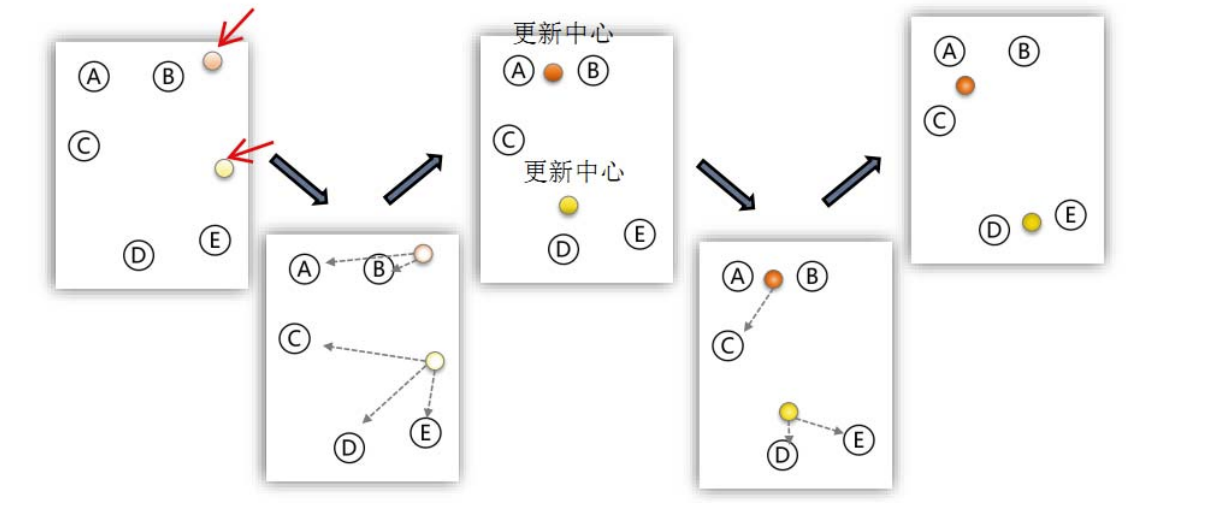
迭代算法如下： 1. 随机得到 K 个初始质心，每一个质心代表一个类 2. 扫描所有样本点，把每个点划归到到离它最近的质心的簇类中 3. 重新计算每个类的质心。 4. 重复 2. 和 3. 5. 直到分类/质心不在发生变化时结束

迭代

迭代

SPSS

SPSS-分析-分类-K均值聚类

缺陷

1. 每次计算需要给定簇数目K
2. 对孤立点（异常点）敏感，（会产生孤立点为单独一类的情况）
3. 对于初始值敏感
4. k-means不能解决非凸（non-convex）数据（不规则形状聚类）

层次(系统)聚类(Hierarchical)

步骤

1. 迭代步骤
   1. 把每个样本作为单独一个类，计算类与类之间的距离，用邻近度矩阵记录
   2. 将邻接矩阵中最小的距离连接的类归为一类
   3. 根据新的类，更新邻近度矩阵（若以类中样本间最短距离为类距离则不需要更新）
   4. 重复2. 3.
   5. 到只只剩下一个类的时候，停止
2. 画出聚类谱系图（SPSS自带）
3. 画出聚合系数折线图
   1. 对于每个聚合类别，计算每个类 $$ 的畸变程度：$$
   2. 计算所有类的总畸变程度，即聚合系数：$$
   3. 以聚合类别数 $$ 为横坐标，以聚合系数 $$ 为纵坐标
4. 通过肘部法则（Elbow Method）判断最优聚合数量，得到聚类结果

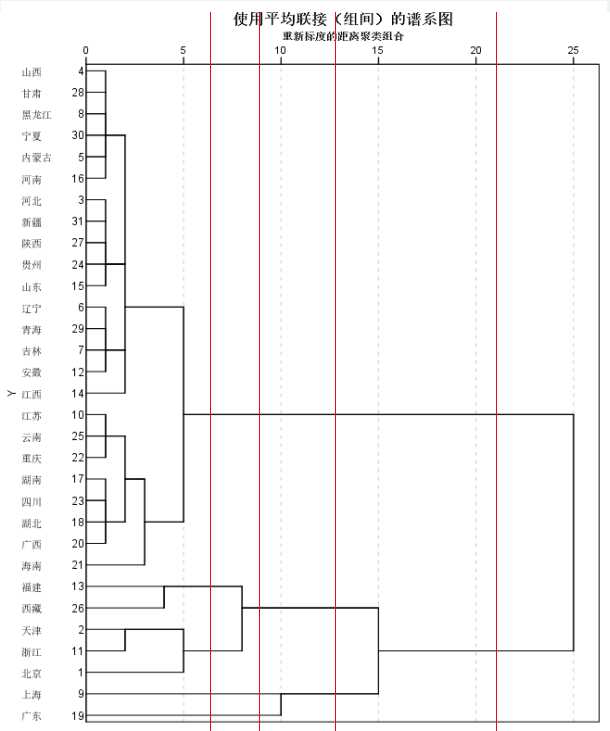
以上是凝聚(agglomerative)途径，即自下而上方法，还可以使用分裂(divisive)的途径。

自下而上法就是一开始每个个体（object）都是一个类，然后根据linkage寻找同类，最后形成一个“类”；自上而下法就是反过来，一开始所有个体都属于一个“类”，然后根据linkage排除异己，最后每个个体都成为一个“类”^[4]。

SPSS

SPSS-分析-分类-系统聚类

基于密度的DBSCAN算法

DBSCAN(Density-based spatial clustering of applications with noise)
是一种基于密度的聚类方法，该方法能在具有噪声的空间数据库中发现任意形状的簇，可将密度足够大的相邻区域连接，能有效处理异常数据。

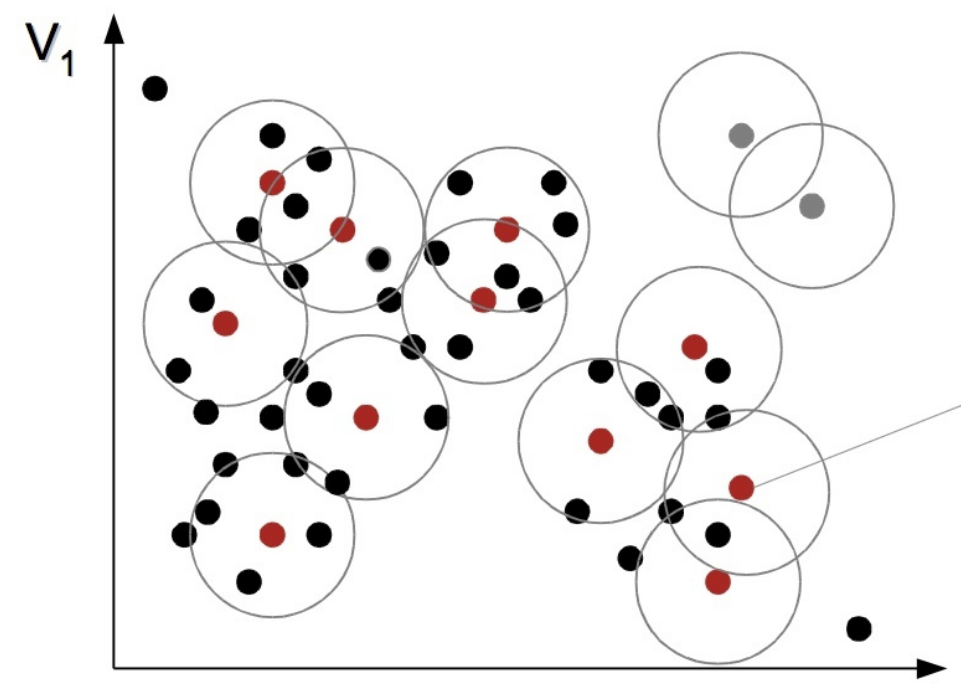
基本概念

• 核心点：在该点半径 $$ 内含的点数不少于 $$
• 边界点：在该点半径 $$ 内点的数量小于 $$，但是落在核心点的半径 $$ 邻域内
• 噪音点：既不是核心点也不是边界点的点，即不在核心点的半径 $$ 邻域内的点

DBSCAN密度聚类可视化

密度聚类

密度聚类

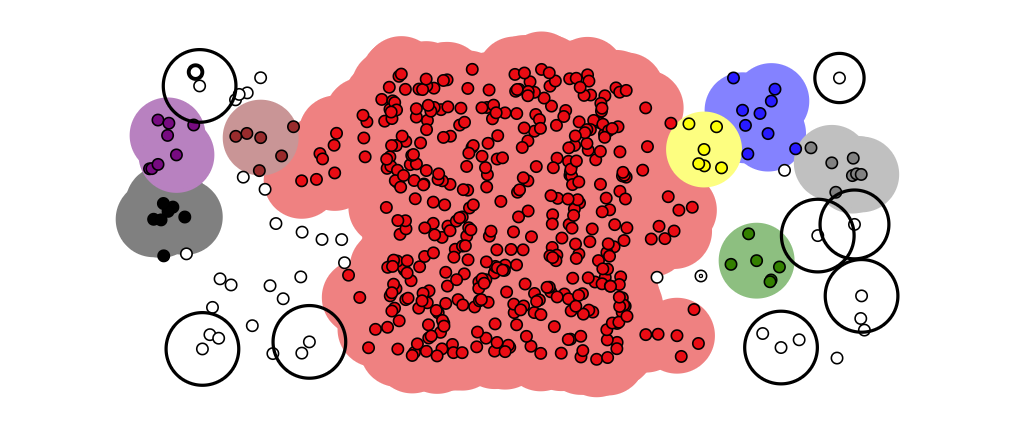
缺点

• 对输入参数 Eps 和 Minpts 敏感，确定参数困难，不同参数相差很大
• 时间复杂度高，处理大量数据时慢

根据网格单元的聚类

其原理是将数据空间划分为网格单元，将数据对象映射到网格单元中，并计算每个单元的密度。根据预设阈值来判断每个网格单元是不是高密度单元，由邻近的稠密单元组成“类”^[3]。

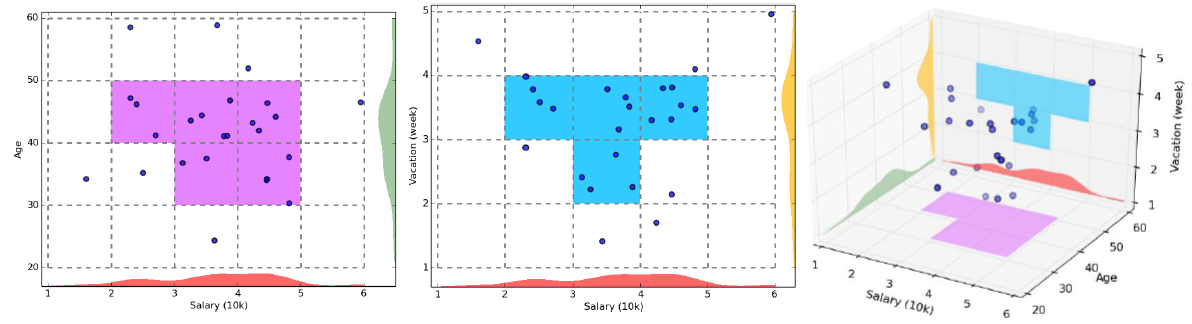
步骤

1.将数据空间划分为网格单元 2.依照设置的阈值，判定网格单元是否稠密 3.合并相邻稠密的网格单元为一类

特点

• 优点
  • 效率快速度快
  • 直观易于理解
• 缺点
  • 拟合较为粗糙，分类不精确，无法处理不规则分布的数据
  • 对输入参数敏感，难以确定方格宽以及稠密阈值，方格宽以及稠密阈值对结果影响很大

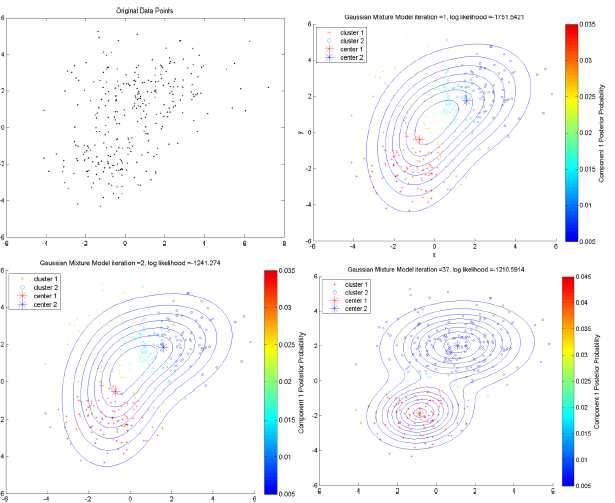
基于概率的聚类

Model-based methods
这一类方法主要是指基于概率模型的方法和基于神经网络模型的方法，尤其以基于概率模型的方法居多。这里的概率模型主要指概率生成模型（generative Model），同一”类“的数据属于同一种概率分布^[4]。

数据简化

• 变换（Data Transformation）：
  • 离散傅里叶变换（Discrete Fourier Transformation）可以提取数据的频域（frequency domain）信息
  • 离散小波变换（Discrete Wavelet Transformation）除了频域之外，还可以提取到时域（temporal domain）信息^[4]
• 降维（Dimensionality Reduction）：
  • 线性方法
    • PCA（Principle Component Analysis）
    • SVD（Singular Value Decomposition）
    • MDS（Multi-Dimensional Scaling）PCA拓展
  • 非线性降维的算法
    • 流形学习（Manifold Learning）
      • ISOMAP、
      • LLE（Locally Linear Embedding）、
      • MVU（Maximum variance unfolding）、
      • Laplacian eigenmaps、Hessian eigenmaps、
      • Kernel PCA、
      • Probabilistic PCA
• 抽样（Sampling）：
  • 随机抽样

三大步骤的综合

对于聚类分析三大步骤：

1. 相似性衡量：距离、相似系数、核函数、DTW（dynamic time warping）
2. 聚类算法：Hierarchical methods、Partition-based methods、Density-based methods、Grid-based methods、Model-based methods
3. 数据简化：变换、降维、抽样

其中每个二级分类下含有多种方法。三个步骤每个选择一个方法可以组合出庞大数量的聚类模型。

例如：谱聚类（Spectral Clustering），就是先用Laplacian eigenmaps对数据降维（简单地说，就是先将数据转换成邻接矩阵或相似性矩阵，再转换成Laplacian矩阵，再对Laplacian矩阵进行特征分解，把最小的K个特征向量排列在一起），然后再使用k-means完成聚类。谱聚类是个很好的方法，效果通常比k-means好，计算复杂度还低，这都要归功于降维的作用^[4]。

参考

• 这里非常感谢知乎答主@郭小天的分享给了我很大启发

1. 司守奎 孙兆亮. 数学建模算法与运用[M]. 第2版. 第216页. ↩︎
2. https://baike.baidu.com/item/%E8%81%9A%E7%B1%BB%E5%88%86%E6%9E%90/3450227 ↩︎
3. https://zhuanlan.zhihu.com/p/37856153 ↩︎
4. https://www.zhihu.com/question/34554321/answer/64372216 ↩︎