分类模型
判别分析是在已知研究对象分成若干类型并已经取得各种类型的一批已知样本的观测数据,在此基础上根据某些准则建立判别式,然后对未知类型的样品进行判别分析。
0-1回归
即采用逻辑回归(logistic regressio)
把观测数据作为因变量对虚拟变量(0,1)进行回归,将y看作事件0发生的概率。
模型构造
构造线性概率模型
\[y_{i}=\beta_{0}+\beta_{1} x_{1 i}+\beta_{2} x_{2 i}+\cdots+\beta_{k} x_{k i}+\mu_{i}\]
㝍成向量乘积形式: \(y_{i}=\boldsymbol{x}_{i}^{\prime} \boldsymbol{\beta}+u_{i}(i=1,2, \cdots, n)\)
构造两点分布
\[\left\{\begin{array}{l} P(y=1 \mid \boldsymbol{x})=F(\boldsymbol{x}, \boldsymbol{\beta}) \\ P(y=0 \mid \boldsymbol{x})=1-F(\boldsymbol{x}, \boldsymbol{\beta}) \end{array} \text { 注: 一般 } F(\boldsymbol{x}, \boldsymbol{\beta})=S\left(\boldsymbol{x}_{\boldsymbol{i}}^{\prime} \boldsymbol{\beta}\right)\right.\]
构造连接函数
要使 \(F(\boldsymbol{x},\boldsymbol{\beta})\) 为值域 \([0,1]\) 上的函数。构造以下函数:
- \(F(\boldsymbol{x},\boldsymbol{\beta})\) 取正态分布累计密度函数\((cdf)\) \[\begin{array}{c} F(\boldsymbol{x}, \boldsymbol{\beta})=\Phi\left(\boldsymbol{x}_{\boldsymbol{i}}^{\prime} \boldsymbol{\beta}\right)=\int_{-\infty}^{\boldsymbol{x}_{\boldsymbol{i}}^{\prime} \boldsymbol{\beta}} \frac{1}{\sqrt{2 \pi}} e^{-\frac{t^{2}}{2}} d t \\ \color{Red} (\text { probit 回归 }) \end{array}\]
- \(F(\boldsymbol{x},\boldsymbol{\beta})\) 取\(Sigmoid\)函数 \[\begin{aligned} F(\boldsymbol{x}, \boldsymbol{\beta})=& S\left(\boldsymbol{x}_{i}^{\prime} \boldsymbol{\beta}\right)=\frac{\exp \left(\boldsymbol{x}_{i}^{\prime} \boldsymbol{\beta}\right)}{1+\exp \left(\boldsymbol{x}_{i}^{\prime} \boldsymbol{\beta}\right)} \\ & \color{Red} (\text{ logistic回归 }) \end{aligned}\]
参数求解
对于非线性模型采用极大似然估计法(MLE)估计: \[f\left(y_{i} \mid \boldsymbol{x}_{i}, \boldsymbol{\beta}\right)=\left\{\begin{array}{ll} S\left(\boldsymbol{x}_{i}^{\prime} \boldsymbol{\beta}\right) & , y_{i}=1 \\ 1-S\left(\boldsymbol{x}_{i}^{\prime} \boldsymbol{\beta}\right) & , y_{i}=0 \end{array}\right.\] 即 \[f\left(y_{i} \mid \boldsymbol{x}_{i}, \boldsymbol{\beta}\right)=\left[S\left(\boldsymbol{x}_{i}^{\prime} \boldsymbol{\beta}\right)\right]^{y_{i}}\left[1-S\left(\boldsymbol{x}_{\boldsymbol{i}}^{\prime} \boldsymbol{\beta}\right)\right]^{1-y_{i}}\] 取对数 \[\ln f\left(y_{i} \mid \boldsymbol{x}_{i}, \boldsymbol{\beta}\right)=y_{i} \ln \left[S\left(\boldsymbol{x}_{i}^{\prime} \boldsymbol{\beta}\right)\right]+\left(1-y_{i}\right) \ln \left[1-S\left(\boldsymbol{x}_{i}^{\prime} \boldsymbol{\beta}\right)\right]\] 得到样本对数似然函数 \[\left.\ln L(\boldsymbol{\beta} \mid \boldsymbol{y}, \boldsymbol{x})=\sum_{i=1}^{n} y_{i} \ln \left[S\left(\boldsymbol{x}_{\boldsymbol{i}}^{\prime} \boldsymbol{\beta}\right)\right]+\sum_{i=1}^{n}\left(1-y_{i}\right) \ln \left[1-S\left(\boldsymbol{x}_{\boldsymbol{i}}^{\prime} \boldsymbol{\beta}\right)\right]\right.\] 求这个函数的最大化。
求准确率
把数据分为训练组和测试组,一般取80%和20%,多次随机抽选训练组和测试组,对模型求一个平均的准确率(交叉验证)。
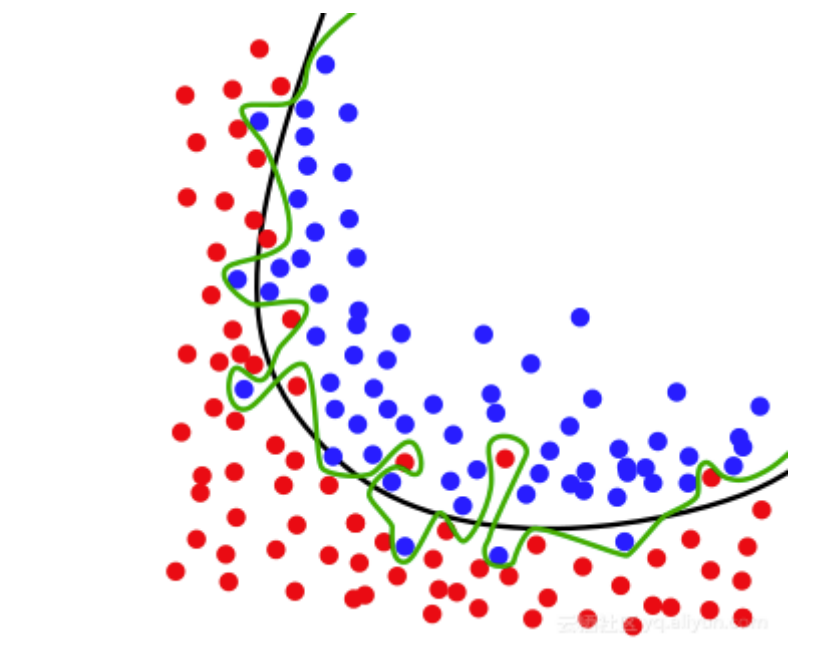
思考
对于这个模型 \(\hat{y}\) 理解为为事件“\(y=1\)”发生的概率
\[\hat{y}_{i}=P\left(y_{i}=1 \mid \boldsymbol{x}\right)=S\left(\boldsymbol{x}_{i}^{\prime} \hat{\boldsymbol{\beta}}\right)=\frac{\exp \left(\boldsymbol{x}_{i}^{\prime} \hat{\boldsymbol{\beta}}\right)}{1+\exp \left(\boldsymbol{x}_{i}^{\prime} \hat{\boldsymbol{\beta}}\right)}=\frac{e^{\widehat{\beta}_{0}+\widehat{\beta}_{1} x_{1 i}+\widehat{\beta}_{2} x_{2 i}+\cdots+\widehat{\beta}_{k} x_{k i}}}{1+e^{\widehat{\beta}_{0}+\widehat{\beta}_{1} x_{1 i}+\widehat{\beta}_{2} x_{2 i}+\cdots+\widehat{\beta}_{k} x_{k i}}}\]
对于 \(S\left(\boldsymbol{x}_{i}^{\prime} \hat{\boldsymbol{\beta}}\right)=\frac{1}{2}\) 即
\[{\widehat{\beta}_{0}+\widehat{\beta}_{1} x_{1 i}+\widehat{\beta}_{2} x_{2 i}+\cdots+\widehat{\beta}_{k} x_{k i}}=0\]
可以看作一个超平面( \(k=2\)时是直线 )。该分类的本质就是找到一个“曲线”把 '\(y=0\)' 和 '\(y=1\)' 分割到曲线的两侧。
Fisher线性判别分析
线性判别式分析(Linear Discriminant Analysis, LDA)
也叫做Fisher线性判别(Fisher Linear Discriminant ,FLD)
基本思想:选取适当的投影方向将高维数据投影到低维空间上使得投影后各样本类内离差平方和尽可能小,而使各样本类间的离差平方和尽可能大[2]。即,使得在子空间上有最佳的可分离性。
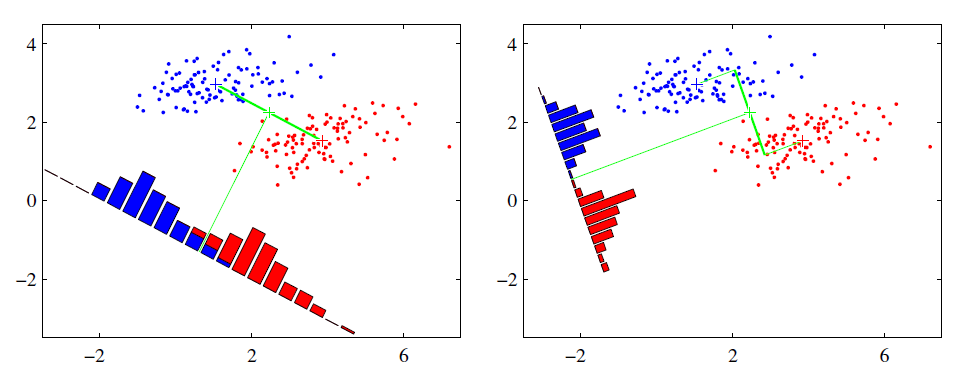
一维压缩的Fisher判别模型
Fisher判别可以将 \(C\) 维指标压缩到 \([1,C-1]\) 纬空间。这里只解释将样本压缩到一维的情况。
设样本数据集为 \(\{\boldsymbol{D_1},\boldsymbol{D_2}\}\) (二维指标), \(\boldsymbol{X_i}\) 是第 \(i\) 类样本的集合 ,\(X_i\) 是第 \(i\) 类样本的集合,第 \(i\) 个集合样本是数目是 \(N_i\) ,\(x=(d_1,d_2)\)。最佳的向量称为 \(\boldsymbol{w}\)[4]。
记 \(\mu_i\) 为第i类样本质心,为 \[\mu_{i}=\frac{1}{N_{i}} \sum_{x \in \boldsymbol{X_{i}}} x\]
\(x\) 到 \(\boldsymbol{w}\) 投影后的样本点均值为
\[\tilde{\mu}_{i}=\frac{1}{N_{i}} \sum_{x \in \boldsymbol{X}_{i}} y=\frac{1}{N_{i}} \sum_{x \in \boldsymbol{X}_{i}} \boldsymbol{w}^{T} x=\boldsymbol{w}^{T} \mu_{i}\]
类间方差最大化,那么就是要让 \(J(\boldsymbol{w})\) 最大
\[J(\boldsymbol{w})=\left|\tilde{\mu}_{1}-\tilde{\mu}_{2}\right|=\left|\boldsymbol{w}^{T}\left(\mu_{1}-\mu_{2}\right)\right|\]
但是只满足这一个条件并不行,两个类达到了类间方差最大化的条件,但是可能轴上的投影两个类重合的部分太多,无法进行有效的区分。
类内方差最小化
对于类内方差,使用另外一个值散列值(scatter),计算方法如果下,其实就是投影值与中心之间的方差和。目的就是使这个值最小。
\[\tilde{s_{i}}^{2}=\sum_{y \in \boldsymbol{Y}_{i}}\left(y-\tilde{\mu}_{i}\right)^{2},(y=\boldsymbol{w}^Tx)\]
最后,我们结合这两个条件
\[J(\boldsymbol{w})=\frac{\left|\tilde{\mu_{1}}-\tilde{\mu_{2}}\right|}{\tilde{s_{1}}^{2}+\tilde{s_{2}}^{2}}\]
我们要做的就是让 \(J(\boldsymbol{w})\) 最大。推导过程
结论:
\[S_{i}=\sum_{x \in \omega_{i}}\left(x-\mu_{i}\right)\left(x-\mu_{i}\right)^{T}\]
\[S_{W}=S_{1}+S_{2}\]
\[\boldsymbol{w}=S_{W}^{-1}\left(\mu_{1}-\mu_{2}\right)\]
思考
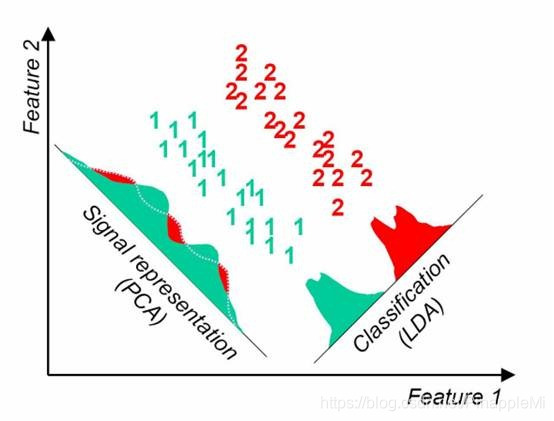
主成分分析(PCA):是找到方差尽可能大的维度,使得信息尽可能都保存,不考虑样本的可分离性,不具备预测功能。
线性判别分析(LAD):是找到一个低维的空间,投影后,使得可分离性最佳(保留信息趋少),投影后可进行判别以及对新的样本进行预测[3]。
相较于压缩至一维空间,压缩到二维平面或超平面上常常更能分离出不同的样本。