模糊综合评价
请注意,本文最后更新于2022.2.1,其中一些理解可能已被笔者推翻或废弃。
模糊综合评价(fuzzy sets)
模糊综合评价(Fuzzy Comprehension Evaluation Method)又为模糊集合理论(fuzzy sets) 对于难以明确分类,边界不明显的评价指标可才用模糊综合评价,模型关键在于构造的隶属函数的准确性和合理性。
基本步骤
建立综合评价的因素集
模糊综合评价指标的构建。
因素集是以影响评价对象的各种因素为元素所组成的一个普通集合,通常用 \(U\) 表示, \(U=(u_1,u_2,\cdots,u_m)\),其中元素 \(u_i\) 代表影响评价对象的第 \(i\)
个因素。这些因素,通常都具有不同程度的模糊性。
建立综合评价的评价集
评价集是评价者对评价对象可能做出的各种结果所组成的集合,通常用 \(V\) 表示, \(V=(v_1,v _2,\cdots,v_m)\) ,其中元素 \(v_i\) 代表第 \(i\) 种评价结果
构造隶属函数,获得评价矩阵
构造合理美观的隶属函数 \(Fuzz(x)\)。
若因素集U中第i个元素对评价集V中第1个元素的隶属度为 \(r_{i1}\) ,则对第 \(i\) 个元素单因素使用隶属函数评价的结果用模糊集合表示为:\(R_i=(r_{i1},r_{i2},\cdots,r_{in})\)。以 \(m\) 个单因素评价集构成 \(R_{mn}=[R1,R2,\cdots,Rm]^T\) ,称为模糊综合评价矩阵。
确定因素权向量
评价工作中,各因素的重要程度有所不同,为此,给各因素 \(u_i\)一个权重 \(w_i\) ,各因素的权重集合的模糊集,用 \(W\) 表示: \(W=(w_1,w_2,\cdots,w_m)\)。
建立综合评价模型
确定单因素评判矩阵 \(R\) 和因素权向量 \(W\) 之后,通过模糊变化将 \(U\)上的模糊向量 \(A\) 变为 \(V\) 上的模糊向量 \(B\),即 \[B=W_{1m}\cdot R_{mn}=(b_1,b_2,\cdots,b_n)\]
绘出结果 \(B\) 图像,如 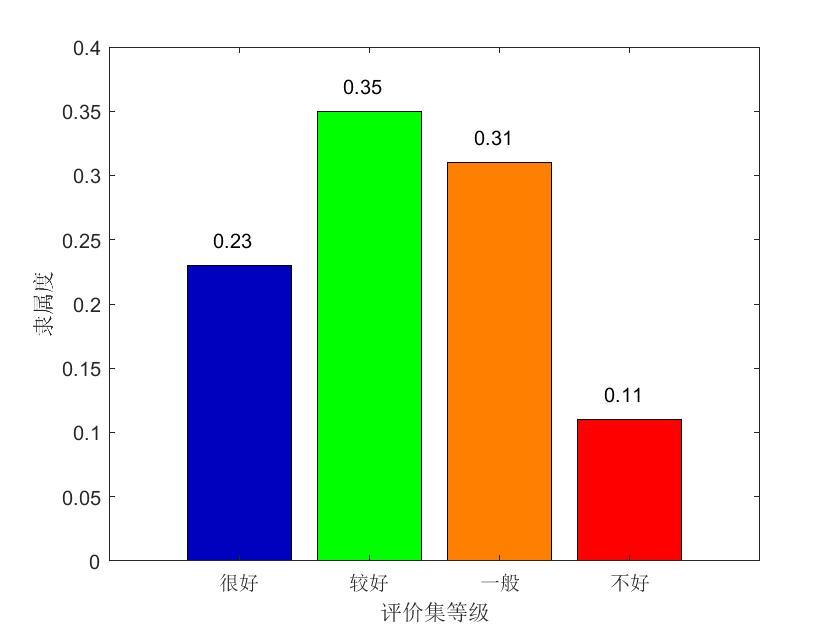
一些思考
对于模糊评价,相较于作为一个“综合评价”,我更愿意把模糊综合评价看作为类似于层次分析法的带有主观意愿的评价(体现在隶属函数的构造上);对于模糊集合理论(模糊数学),更愿意看作一种思想(隶属程度的思想)。
在2021亚太杯C题的第三四题中我用模糊数学思想,对于“是否属于城市印象范围”构造了这样的“模糊隶属函数”。\(Fuz_1(x)=\frac{ℯ^{-(k(x-b))}}{ℯ^{-(k(x-b))}+1}\)、\(Fuz_2(x)=ℯ^{\frac{(x-a)^2}{q}}\) 得到了以下的结果。 (22.2.1)
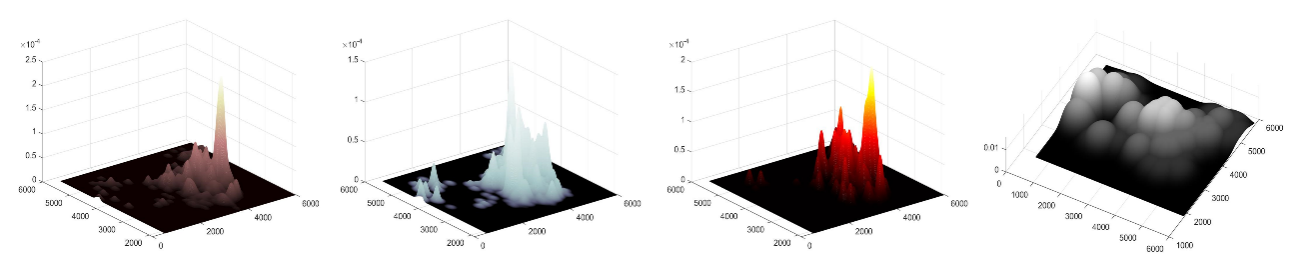
参考
[^1] https://baike.baidu.com/item/%E6%A8%A1%E7%B3%8A%E7%BB%BC%E5%90%88%E8%AF%84%E4%BB%B7%E6%B3%95/2162444 [^2] https://zhuanlan.zhihu.com/p/32666445