层次分析法
请注意,本文最后更新于2022.2.1,其中一些理解可能已被笔者推翻或废弃。
层次分析法(AHP)
层次分析法(Analytic Hierarchy Process,AHP)
这是一种定性和定量相结合的、系统的、层次化的分析方法。这种方法是在对复杂决策问题的本质上,利用较少的定量信息使决策的思维过程数学化,从而为多目标、多准则或无结构特性的决策问题提供简便的决策方法。是对难以定量的复杂系统进行决策的模型。
层次分析法的根本是打分法:确定指标,不同方案指标打分,为指标确定权重。用于处理数据未知的评价。
层次分析法将问题分解为组成因素,并按照因素间关联、影响以及隶属关系将因素按不同的层次聚集组合,形成一个多层次的分析结构模型。从而最终使问题归结为最低层(供决策的方案、措施等)相对于最高层(总目标)的相对重要权值的确定或相对优劣次序的排定。
基本步骤
建立层次模型
思考以下问题:
- 我的的评价目标是什么?
- 达到目标有哪些方案?
- ★对方案的评价准则或指标是什么?(最好参考引用文献)
将决策的目标、决策准则(考虑的因素)和决策对象绘制为层次结构图。
- 最高层(目标层):决策的目的、要解决的问题;
- 中间层(准则层或指标层):考虑的因素、决策的准则;
- 最低层(方案层):决策时的备选方案;
或仅绘制评价体系(树状图或表格)如下 (要包含多级指标):
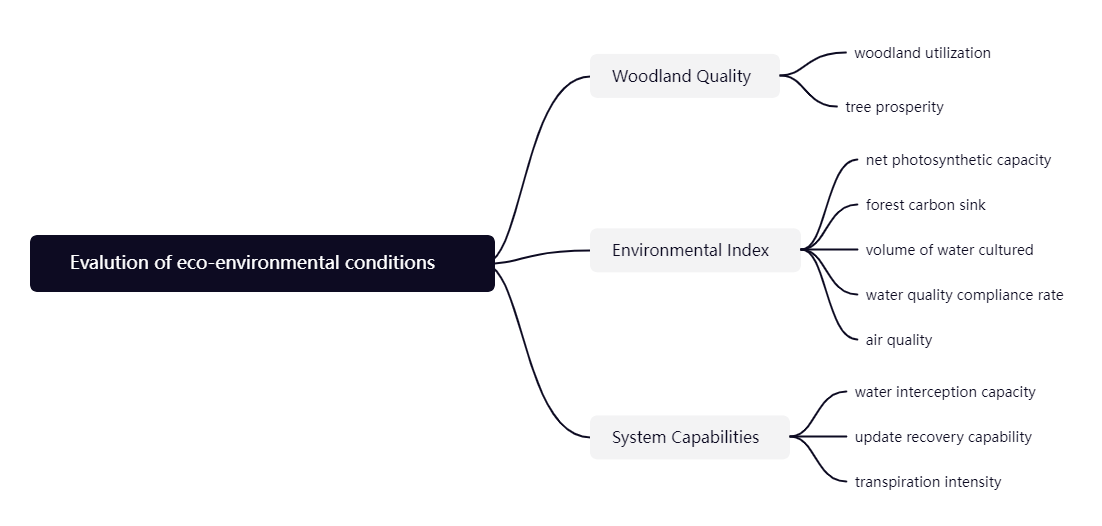
构造判断矩阵
(成对比较矩阵)
在确定权重时,只给出定性的结果(就是我认为景色占80%,费用10%等等),常常不被别人接受,因此采用一致矩阵法,即:
- 不把所有因素放在一起比较,而是两两比较
- 对此时采用相对尺度,尽可能减少诸因素导致的相互比较的困难,提高准确性
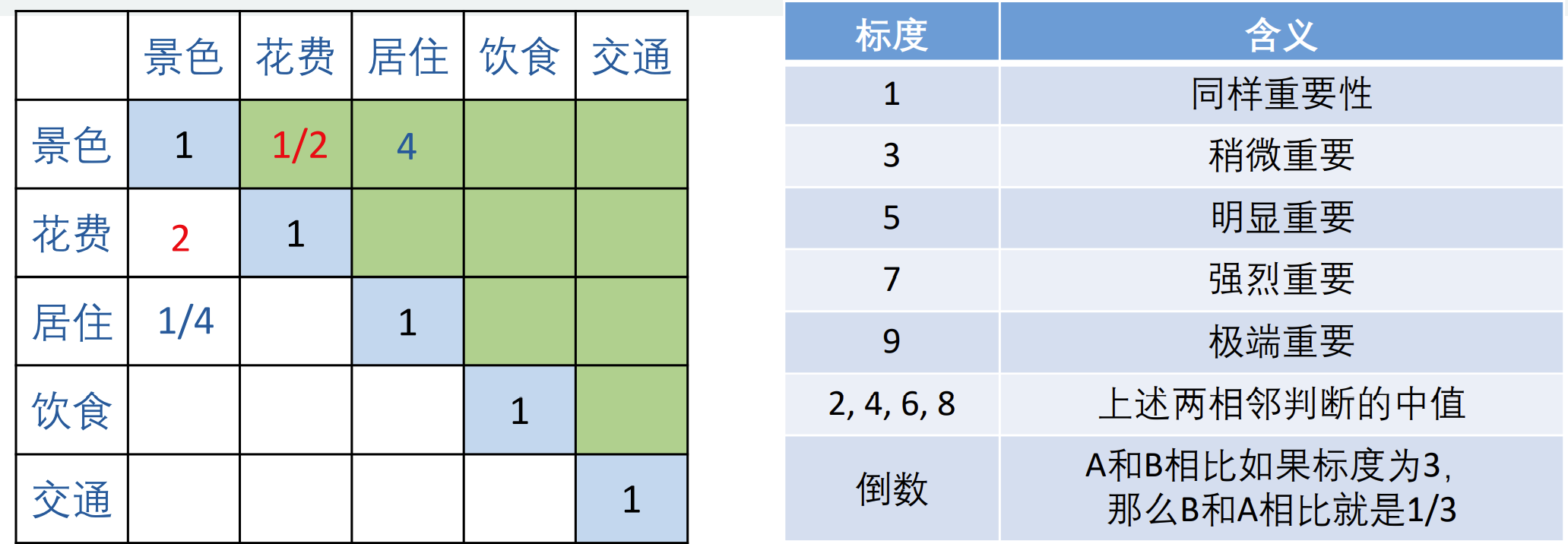
成对比较矩阵是表示本层所有因素针对上一层某一个因素(准侧或目标)的相对重要性的比较。成对比较矩阵的元素 \(a_{ij}\) 表示的是第 \(i\) 个因素相对于第 \(j\) 个因素的比较结果,这个值使用的是Santy的1-9标度方法给出。
定义且满足
\[a_{ij}=i相对j的重要度=\frac{i的重要程度}{j的重要程度}=a_{ik}a_{kj}\]
一致性检验
\(\left[\begin{array}{cccc} a_{11} & a_{12} & \cdots & a_{1 n} \\ a_{21} & a_{22} & \cdots & a_{2 n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n 1} & a_{n 2} & \cdots & a_{n n} \end{array}\right]\)为一致矩阵的充要条件\(\left\{\begin{array}{l} a_{i j}>0 \\ a_{11}=a_{22}=\cdots=a_{n n}=1 \\ {\left[a_{i 1},..., a_{i n}\right]=k_{i}\left[a_{11},..., a_{1 n}\right]} \end{array}\right.\)
对于
一致阵:则我们自然会取对应于最大特征根 \(n\) 的归一化特征向量 \(\{w_1,w_2,\cdots,w_n\}\) ,且 \(\sum_{i=1}^{n}{w_i=1}\) , \(w_i\) 表示下层第 \(i\) 个因素对上层某个因素影响程度的权值。
非一致阵:用其最大特征根对应的归一化特征向量作为权向量 \(W=\{w_1,w_2,\cdots,w_n\}\) ,则 \(AW=\lambda W\) ,这样确定权向量的方法称为特征根法;
定理:
- \(n\) 阶一致阵的唯一非零特征根为 \(n\)
- \(n\) 阶互反阵 \(A\left(a_{i j}>0, a_{i j}=\frac{1}{a_{j i}}, a_{i i}=1\right)\) 最大特征根 \(\lambda \geq n\) ,当且仅当 \(\lambda=n\) 时, \(A\) 为一致矩阵。
\(\lambda\) 连续的依赖于 \(a_{ij}\) ,则 \(\lambda\) 比 \(n\) 大的越多, \(A\) 的不一致性越严重。用最大特征值对应的特征向量作为影响程度的权向量,其不一致程度越大,引起的判断误差越大。
第一步:计算一致性指标CI
\[CI=\frac{\lambda -n}{n-1}\]
- \(CI=0\) ,有完全的一致性;
- \(CI\) 接近 \(0\) ,有满意的一致性
- \(CI\) 越大,不一致越严重;
第二步:查找对应的平均随机一致性指标RI
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RI | 0 | 0 | 0.52 | 0.89 | 1.12 | 1.26 | 1.36 | 1.41 | 1.46 | 1.49 | 1.52 | 1.54 | 1.56 | 1.58 | 1.59 |
\(RI\) 为统计结果,详细计算方法参考这里
第三步:计算一致性比例CR
\[CR=\frac{CI}{RI}\]
如果 \(CR < 0.1\), 则可认为判断矩阵的一致性可以接受;否则需要对判断矩阵进行修正。
求得权重
- 算术平均法求权重 \[\omega_{i}=\frac{1}{n} \sum_{j=1}^{n} \frac{a_{i j}}{\sum_{k=1}^{n} a_{k j}}\]
- 几何平均法求权重 \[\omega_{i}=\frac{\left(\prod_{j=1}^{n} a_{i j}\right)^{\frac{1}{n}}}{\sum_{k=1}^{n}\left(\prod_{j=1}^{n} a_{k j}\right)^{\frac{1}{n}}}\]
- 特征值法求权
特别的:若特征值为n,对应特征向量为\(k\left[\frac{1}{a_{11}}, \frac{1}{a_{12}}, \cdots, \frac{1}{a_{1 n}}\right]^{T}\),且特征向量刚好为矩阵第一列。
假如我们的判断矩阵一致性可以接受,那么我们可以仿照一致矩阵权重的求法。
- 求出矩阵A的最大特征值以及其对应的特征向量
- 对求出的特征向量进行归一化即可得到我们的权重( \(\sum_{i=1}^{n}{w_i=1}\) )
填表得结果
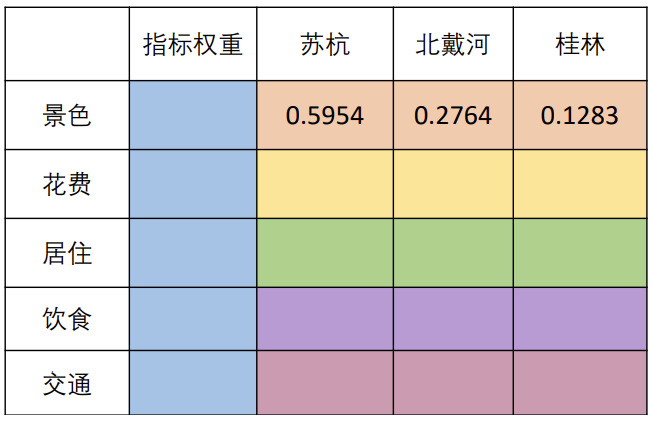
然后相应的加权计算得分即可得到结果。
一点补充
详细做法补充
- 对于评价指标:
- 单层评价指标:构造所有指标的两两判断矩阵,得到权值
- 多层评价指标:
- 构造一级指标的两两判断矩阵,得到权值
- 构造每个一级指标下的二级指标的两两判断矩阵(每个一级指标一个矩阵),得到权值
- 构造每个二级指标下……
……
- 对于方案:
- 对于每个最低级指标构造所有方案的两两判断矩阵,得到权值
示例:
\[ \left\{\begin{array}{l} 一级指标1\left\{\begin{array}{l} 二级指标1 :a_{11},a_{12},a_{13}\\ 二级指标2 :a_{21},a_{22},a_{23}\\ \end{array}\right.\\ \\ 一级指标2\left\{\begin{array}{l} 二级指标3 :a_{31},a_{32},a_{33}\\ 二级指标4 :a_{41},a_{42},a_{43}\\ 二级指标5 :a_{51},a_{52},a_{53}\\ \end{array}\right.\\ \\ 一级指标3 : a_{61},a_{62},a_{63} \end{array}\right.\\ \]
特征向量含义思考
对于矩阵 \(A=\left[\begin{array}{cccc} a_{11} & a_{12} & \cdots & a_{1 n} \\ a_{21} & a_{22} & \cdots & a_{2 n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n 1} & a_{n 2} & \cdots & a_{n n} \end{array}\right]\) , \(W=\left[\begin{array}{c} w_{1}\\ w_{2}\\ \vdots\\ w_{n} \end{array}\right]\) ,满足 \(AW=\lambda A\) 。
矩阵的本质是变换,把 \(A\) 看作对 \(m\) 纬空间单位球体进行 \(A\) 变换,取 \(\lambda\) 最大时的特征向量 \(W\) ,即表示为变换后的球体上与变换前方向相同的点中距离原点 \(O\) 最远的点(距离原点距离为 \(\lambda\) )所表示的方向向量 。记 \(W\) 为可以代表整个变换 \(A\) 的线性变换。
特别的对于对称矩阵 \(A\) ,变换 \(A\) 一定是将球变为椭球,这也是不同特征值对应特征向量一定正交的原因,相同特征值 \(\lambda\) 若有多个特征向量 \(e_1,e_2,...\),特征向量的张成空间都是该特征值 \(\lambda\) 的特征向量。\(\lambda\) 的特征向量。
但是,对于非特殊矩阵,几何意义不明确,另外对于正互反矩阵、一致性矩阵的变换性质,笔者并不清楚,所以也仅仅能近似的类比理解到这里了。 (22.1.18)
一些问题
- 评价的决策层不能太多,太多的话n会很大,判断矩阵和一致矩阵差异可能会很大。
- 平均随机一致性指标RI的表格中n最多是15。
所以当n过大可以分层归纳为多级指标再构造多个判断矩阵。